解不等式:
(1)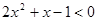 (2)
(2)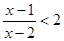
已知椭圆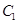 的方程为
的方程为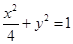 ,双曲线
,双曲线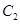 的左、右焦点分别为
的左、右焦点分别为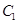 的左、右顶点,而
的左、右顶点,而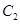 的左、右顶点分别是
的左、右顶点分别是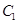 的左、右焦点。
的左、右焦点。
(1)求双曲线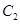 的方程;
的方程;
(2)若直线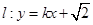 与椭圆
与椭圆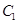 及双曲线
及双曲线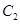 都恒有两个不同的交点,且L与的两个焦点A和B满足
都恒有两个不同的交点,且L与的两个焦点A和B满足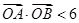 (其中O为原点),求
(其中O为原点),求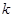 的取值范围。
的取值范围。
如图,三棱柱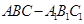 中,
中,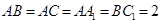 ,
,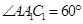 ,平面
,平面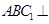 平面
平面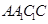 ,
,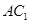 与
与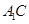 相交于点
相交于点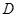 .
.
(Ⅰ)求证: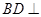 平面
平面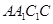 ;
;
(Ⅱ)求二面角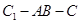 的余弦值.
的余弦值.
已知向量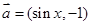 ,
,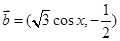 ,函数
,函数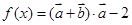 .
.
(1)求函数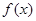 的最小正周期
的最小正周期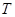 与值域;
与值域;
(2)已知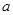 ,
,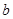 ,
,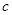 分别为
分别为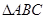 内角
内角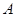 ,
, 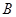 ,
,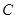 的对边,其中
的对边,其中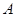 为锐角,
为锐角,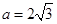 ,
, ,且
,且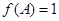 ,求
,求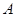 ,
,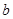 和
和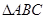 的面积
的面积 .
.
(本小题满分7分)选修4—5:不等式选讲
已知函数 .
.
(Ⅰ)求函数 的值域;
的值域;
(Ⅱ)设 ,试比较
,试比较 与
与 的大小.
的大小.
(本小题满分7分)《选修4-4:坐标系与参数方程》
已知曲线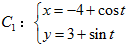 (
(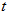 为参数),
为参数),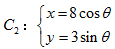 (
(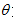 为参数).
为参数).
(Ⅰ)化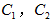 的方程为普通方程;
的方程为普通方程;
(Ⅱ)若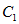 上的点对应的参数为
上的点对应的参数为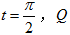 为
为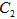 上的动点,求
上的动点,求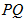 中点
中点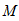 到直线
到直线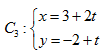 (
(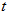 为参数)距离的最小值.
为参数)距离的最小值.