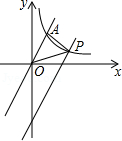
如图,在⊙O中,弦CD垂直于直径AB于点F,OF=3,CD=8,M是OC的中点,AM的延长线交⊙O于点E,DE与BC交于点N,(1)求AB的长;(2)求证:BN=CN.
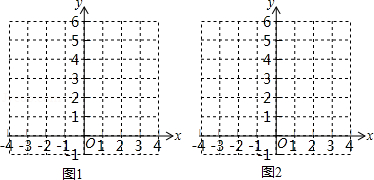
如图1,在平面直角坐标系xOy中,点A的坐标为(0,1),取一点B(b,0),连接AB,作线段AB的垂直平分线l1,过点B作x轴的垂线l2,记l1,l2的交点为P.
(1)当b=3时,在图1中补全图形(尺规作图,不写作法,保留作图痕迹);
(2)小慧多次取不同数值b,得出相应的点P,并把这些点用平滑的曲线连接起来发现:这些点P竟然在一条曲线L上!
①设点P的坐标为(x,y),试求y与x之间的关系式,并指出曲线L是哪种曲线;
②设点P到x轴,y轴的距离分别是d1,d2,求d1+d2的范围,当d1+d2=8时,求点P的坐标;
③将曲线L在直线 下方的部分沿直线y=2向上翻折,得到一条“W”形状的新曲线,若直线 与这条“W”形状的新曲线有4个交点,直接写出k的取值范围.
阅读理解:
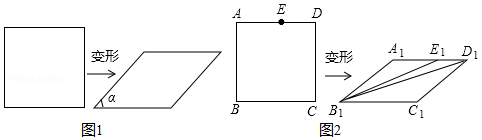
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把 的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形度是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, 之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且 ,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为 ,平行四边形A1B1C1D1的面积为 ,试求∠A1E1B1+∠A1D1B1的度数.
某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
如图,在△ABC中, ,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若 , ,求阴影部分的面积(结果保留π).

如图,在平面直角坐标系中,直线y=2x与反比例函数 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数 在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.