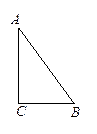阅读理解：
我们知道，四边形具有不稳定性，容易变形，如图1，一个矩形发生变形后成为一个平行四边形，设这个平行四边形相邻两个内角中较小的一个内角为α，我们把 的值叫做这个平行四边形的变形度．
（1）若矩形发生变形后的平行四边形有一个内角是120度，则这个平行四边形的变形度是 ．
猜想证明：
（2）设矩形的面积为S1，其变形后的平行四边形面积为S2，试猜想S1，S2， 之间的数量关系，并说明理由；
拓展探究：
（3）如图2，在矩形ABCD中，E是AD边上的一点，且 ，这个矩形发生变形后为平行四边形A1B1C1D1，E1为E的对应点，连接B1E1，B1D1，若矩形ABCD的面积为 ，平行四边形A1B1C1D1的面积为 ，试求∠A1E1B1+∠A1D1B1的度数．
（本题8分）某市甲、乙两个汽车销售公司，去年一至十月
份每月销售同种品牌汽车的情况如图所示：
（
1）请你根据统计图填写下表：
| 公司 |
平均数 |
方差 |
中位数 |
众数 |
| 甲 |
9 |
|||
| 乙 |
9 |
17.0 |
8 |
（2）请你从以下两个不同的方面对甲、乙两个汽车
销售公司去年一至十月份的销售情况进行分析：
①从平均数和方差结合看；
②从折线图上甲、乙两个汽车销售公司销售数量的
趋势看（分析哪个汽车销售公司较有潜力）。
（本题6分）如图，△ABC中，AC的
垂直平分线DE交AC
于点E，交BC于点D, 若AB＝DC，∠C＝35°，求∠B的度数。
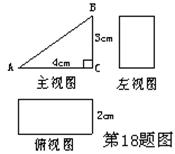
（本题6分）已知一个几何体的三视图和有关尺寸如图所示，其中主视图为直角三角形，
∠ACB=Rt∠，说出这个几何体的名称，并求出这个几何体的表面积。
 |
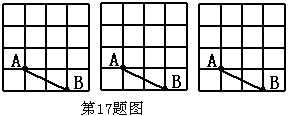
（本题6分）请在下图方格中画出三个以AB为腰的等腰DABC（要求：1、锐角三角形、直角三角形、钝角三角形各画一个；2、点C在格点上）。
 |
(12分)如图，△ABC中,∠C=Rt∠，AB=5cm
，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1㎝，设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长。
(2)问t为何值时，
△BCP是以BC为腰的等腰三角形？
(3)另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2㎝，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动。当t为何值时，直线PQ把△ABC的周长分成相等的两部分？