如图,在平面直角坐标系 中,已知抛物线
中,已知抛物线 经过
经过 ,
, 两点,顶点为
两点,顶点为 .
.
(1)求 、
、 的值;
的值;
(2)将 绕点
绕点 顺时针旋转90°后,点A落到点C的位置,该抛物线沿
顺时针旋转90°后,点A落到点C的位置,该抛物线沿 轴上下平移后经过点
轴上下平移后经过点 ,求平移后所得抛物线的表达式;
,求平移后所得抛物线的表达式;
(3)设(2)中平移后所得的抛物线与 轴的交点为
轴的交点为 ,顶点为
,顶点为 ,若点
,若点 在平移后的抛物线上,且满足△
在平移后的抛物线上,且满足△ 的面积是△
的面积是△ 面积的3倍,求点
面积的3倍,求点 的坐标.
的坐标.
如图所示,一旗杆在离地面5 处折断倒下,旗杆顶部落在离旗杆底部12
处折断倒下,旗杆顶部落在离旗杆底部12  处,求出旗杆在折断之前有多高?
处,求出旗杆在折断之前有多高?
如图所示正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(—4,5),(—1,3).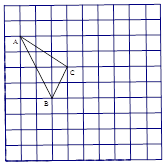
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出三角形ABC关于y轴对称的三角形A’B’C’;
(3)写出点B’的坐标.
如图①,在平面直角坐标系中,直线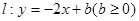 的位置随b的不同取值而变化.
的位置随b的不同取值而变化.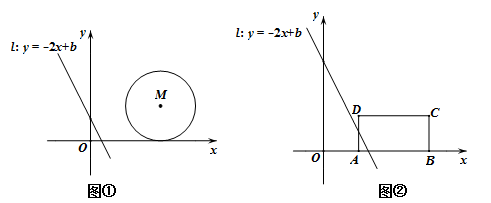
(1)已知⊙M的圆心坐标为(4,2),半径为2,
当b=时,直线 经过圆心M ;
经过圆心M ;
当b=时,直线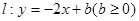 与 ⊙M相切;
与 ⊙M相切;
(2)若把⊙M换成矩形ABCD,如图②,其三个顶点的坐标分别为:A(2,0),B(6,0),C(6,2) .设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.
问题提出:平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考:设不在同一条直线上的三点A、B、C确定的圆为⊙O.
(1)当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是;
如图②,若点D在⊙O内,此时有∠ACB∠ADB;
如图③,若点D在⊙O外,此时有∠ACB∠ADB.(填“=”、“>”或“<”);
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件:.
类比学习:(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.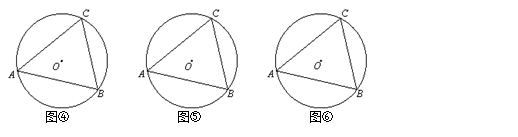
如图④,此时有,
如图⑤,此时有,
如图⑥,此时有.
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件:
.
拓展延伸:(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图,AB是⊙O的直径,点C在⊙O上.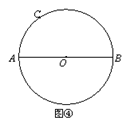
求作:CN⊥AB.
作法:①连接CA,CB;
②在 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
如图1,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D是BC上一定点.动点P从C出发,以2cm/s的速度沿C→A→B方向运动,动点Q从D出发,以1cm/s的速度沿D→B方向运动.点P出发5 s后,点Q才开始出发,且当一个点达到B时,另一个点随之停止.图2是当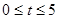 时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.
时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.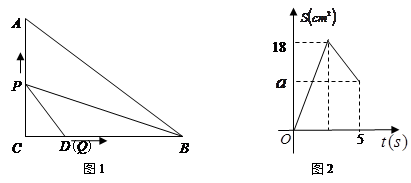
(1)CD =,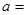 ;
;
(2)当点P在边AB上时,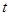 为何值时,使得△BPQ与△ABC为相似?
为何值时,使得△BPQ与△ABC为相似?
(3)运动过程中,求出当△BPQ是以BP为腰的等腰三角形时的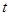 值.
值.