有一个二次函数的图象,三位学生分别说出了它的一些特点.
甲:对称轴是直线x=4;
乙:与x轴两交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3;
请写出满足上述全部特点的二次函数解析式: .
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题: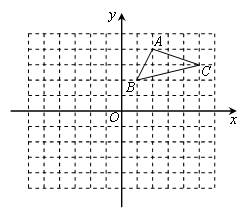
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
解不等式组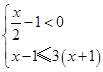 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF,交于点P,请你写出AE与DF的关系,并说明理由;
(2)如图②,当点E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)的结论还成立吗?(请直接回答“是”或“否”,不须证明)
(3)如图③,当E、F分别在CD、BC的延长线上移动时,连接AE和DF,(1)的结论还成立吗?请说明理由;
(4)如图④,当E、F分别在DC、CB上移动时,连接AE和DF交于点P,由于点EF的移动,使得点P也随之运动,请你画出点P的运动路径的草图,若AD=2,试求出线段CP的最小值.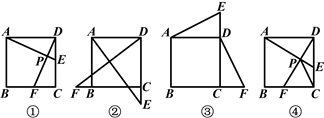
如图,A,P,B,C是⊙O上的四点,∠APC=∠BPC=60°,过点A作⊙O的切线交BP的延长线于点D.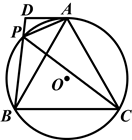
(1)求证:△ADP∽△BDA;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)若AD=2,PD=1,求线段BC的长.
如图,一次函数y=kx+b(k≠0)的图象过点P(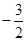 ,0),且与反比例函数
,0),且与反比例函数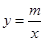 (m≠0)的图象相交于点A(-2,1)和点B.
(m≠0)的图象相交于点A(-2,1)和点B.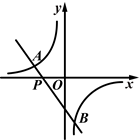
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?