“校园手机”现象越来越受到社会的关注，小刘同学随机调查了某一学校若干学生和家长对中学生带手机现象的看法，制作了如下的统计图：
（1）求这次调查的总人数，并补全条形统计图；
（2）求扇形图中表示家长“赞成”的圆心角的度数；
（3）针对随机调查的情况，小刘决定从初三一班表示赞成的3位家长中随机选择2位进行 深入调查，其中包含小亮和小丁的家长，请你利用画树状图的方法，求出小亮和小丁的家长被同时选中的概率．
先化简，再求值
，其中x＝
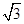－1．
计算：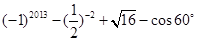
．
如图
，在平面直角坐标系中，等腰直角
的斜边
在
轴上，顶点
的坐标为
，
为斜边上的高．抛物线
与直线
交于点
，点
的横坐标为
．点
在轴的正半轴上，过点作
轴．交射线
于点
．设点的横坐标为
，以
为顶点的四边形的面积为
．
（1）求所在直线的解析式；
（2）求
的值；
（3）当
时，求与的函数关系式；
（4）如图
，设直线
交射线
于点
，交抛物线于点
．以
为一边，在的右侧作矩形
，其中
．直接写出矩形与重叠部分为轴对称图形时的取值范围．
某商店经营儿童益智玩具，已知成批购进时的单价是20元.调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件玩具售价不能高于40元. 设每件玩具的销售单价上涨了x元时（x为正整数），月销售利润为y元.
（1）求y与x的函数关系式并直接写出自变量x的取值范围；
（2）每件玩具的售价定为多少元时，月销售利润恰为2520元？
（3）每件玩具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
如图，△ABC内接于⊙O，直径BD交AC于E，过O作FG⊥AB，交AC于F，交AB于H，交⊙O于G．
（1）求证：OF•DE=2OE•OH；
（2）若⊙O的半径为12，且OE：OF：OD=2：3：6，求阴影部分的面积．（结果保留根号）