有四张背面相同的纸牌A、B、C、D，其正面分别画有四个不同的几何图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．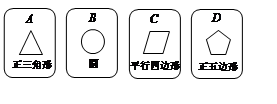
（1）用画树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；
（2）求摸出两张牌面图形都是中心对称图形的纸牌的概率．
先化简，再求值：（本题8分）求
的值，其中
.
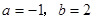解方程：（每题4分，共8分）
（1）4—3（2一x）="5x"
（2）
－
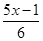=1
化简：（每小题4分，共8分）
（1）
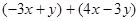
（2）
如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与x轴相交于点A（－３，０），与y轴交于点B，且与正比例函数y=
的图象交点为C（m，4）求：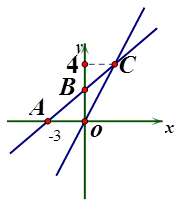
（1）一次函数y=kx+b的解析式；
（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，直接写出点D的坐标。
（3）在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
（1）如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
（2）若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.