先化简,再请你用喜爱的数代入求值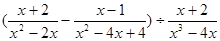
计算: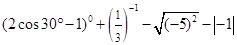
如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
(1)点A的坐标是:_________,点C的坐标是:__________;
(2)设△OMN的面积为S,求S与t的函数关系式;
(3)探求(2)中得到的函数S有没有最大值?若有,求出最大值;若没有,说明理由.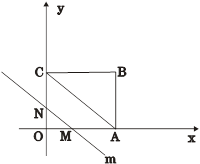
如图,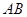 为
为 直径,且弦
直径,且弦 于
于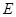 ,过点
,过点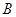 的切线与
的切线与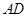 的延长线交于点
的延长线交于点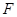 .
.
(1)若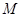 是
是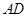 的中点,连接
的中点,连接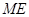 并延长
并延长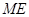 交
交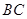 于
于 .求证:
.求证: ;
;
(2)若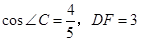 ,求
,求 的半径.
的半径.
我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%,90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.