已知，△ABC为等边三角形，点D为直线BC上一动点（点D不与B、C重合）．以AD为边作菱形ADEF，使∠DAF=60°，连接CF．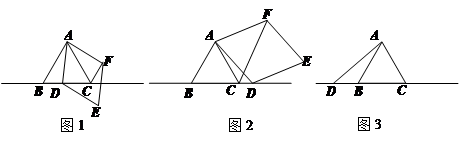
（1）如图1，当点D在边BC上时，
①求证：∠ADB=∠AFC；②请直接判断结论∠AFC=∠ACB＋∠DAC是否成立；
（2）如图2，当点D在边BC的延长线上时，其他条件不变，结论∠AFC=∠ACB＋∠DAC是否成立？若不成立，请写出∠AFC、∠ACB、∠DAC之间存在的数量关系，并写出证明过程；
（3）如图3，当点D在边CB的延长线上时，且点A、F分别在直线BC的异侧，其他条件不变，请补全图形，并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系．
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CAB=2∠CBF．
（1）试判断：直线BF与⊙O的位置关系，并说明理由；
（2）若AB=6，BF=8，求tan∠CBF．
一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10．
（1）求直线AB与CF之间的距离；
（2）求CD的长．
甲、乙两个袋中均装有三张除标数值外完全相同的卡片，甲袋中的三张卡片上所标的数值为﹣7，﹣1，3，乙袋中的三张卡片所标的数值为﹣2，1，6，先从甲袋中随机取出一张卡片，用x表示取出的卡片上的数值，再从乙袋中随机取出一张卡片，用y表示取出卡片上的数值，把x、y分别作为点A的横坐标和纵坐标．
（1）用列表或画树形图的方法写出点A（x，y）的所有的情况；
（2）在题（1）的所有点中随机抽取一点，试求出该点落在直线y=2x上的概率．
如图，在等边△ABC中，点D，E分别在边BC，AB上，且BD=AE，AD与CE交于点F．
（1）求证：AD=CE；
（2）求∠DFC的度数．
为了迎接2015宿迁市“市长杯”阳光体育联赛，丰富学生的课外活动，我县某校团委对部分学生进行了一次问卷调查“你最喜欢的体育活动是什么？”（每人限选一项）．根据收集到的数据，绘制如图统计图（不完整）：请根据图中提供的信息，完成下列问题：
（1）在这次问卷调查中，一共抽查了名学生；
（2）请将条形统计图补充完整；
（3）若全校有1860名学生，则全校学生中，最喜欢“球类”活动学生约有多少人？