如图（1），在平面直角坐标系中，矩形ABCO，B点坐标为（4，3），抛物线y＝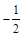
x2＋bx＋c经过矩形ABCO的顶点B、C，D为BC的中点，直线AD与y轴交于E点，点F在直线AD上且横坐标为6．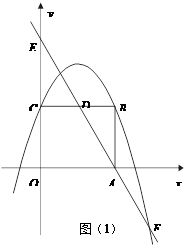
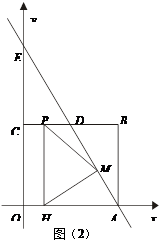
（1）求该抛物线解析式并判断F点是否在该抛物线上；
（2）如图，动点P从点C出发，沿线段CB以每秒1个单位长度的速度向终点B运动；
同时，动点M从点A出发，沿线段AE以每秒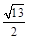
个单位长度的速度向终点E运动．过点P作PH⊥OA，垂足为H，连接MP，MH．设点P的运动时间为t秒．
①问EP＋PH＋HF是否有最小值，如果有，求出t的值；如果没有，请说明理由．
②若△PMH是等腰三角形，求出此时t的值．
(本题满分10分)2010年我国北方冬麦区遭遇本世纪最严重的干旱．为支援抗旱救灾，某水泵制造厂义务承担了生产240台抽水机的任务，由甲、乙两个每个车间承担，已知甲车间单独生产这批抽水机的时问比乙车问单独生产这批抽水机的时问多5天．乙车间每天生产抽水机的数量是甲车间的1.5倍，则甲、乙两车间单独生产这批抽水机各需多少天？
(本题满分8分)已知关于x的一元二次方程x2＋4x＋m－1＝0．(1)请你为m选取一个合适的整数，使方程有两个不相等的实数根．
(2)设α、β是(1)中你所得到的方程的两个实数根．求α2＋β2＋αβ的值．
(本题满分8分)如图①和图②中每个小正方形的边长都为1个单位长度．
(1)将图①中的格点△ABC(顶点都在网格线交点处的三角形叫做格点三角形)向上平移2个单位长度得到△A1B1C1．请你在图①中画出A1B1C1．
(2)在图②中画一个与格点△ABC相似的格点△A2B2C2，且△A2B2C2与△ABC的相似比为2：1．
(本题满分6分)(1)化简：
．(2)解方程：(x＋3)(x＋1)＝6x＋4．
（本题9分）如图(1)，在直角梯形OABC中，BC∥OA，∠OCB＝90°，OA＝6，AB＝5，cos∠OAB＝
．
(1)写出顶点A、B、C的坐标；
(2)如图(2)，点P为AB边上的动点（P与A、B不重合），PM⊥OA，PN⊥OC，垂足分别为M，N．设PM＝x，四边形OMPN的面积为y．
①求出y与x之间的函数关系式，并写出自变量x的取值范围；
②是否存在一点P，使得四边形OMPN的面积恰好等于梯形OABC的面积的一半？如果存在，求出点P的坐标；如果不存在，说明理由．