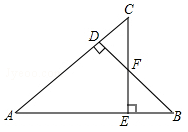
操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点(不包括射线的端点).如图1,2,3是旋转三角板得到的图形中的3种情况.
研究: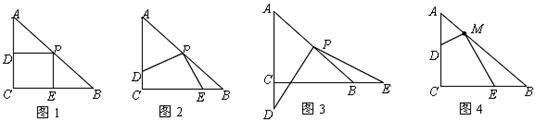
⑴三角板绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合如图2加以证明.
⑵三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长;若不能,请说明理由.
⑶若将三角板的直角顶点放在斜边AB上的M处,且AM∶MB=1∶3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合如图4加以证明.
如图,在△ABC中,AD平分∠BAC.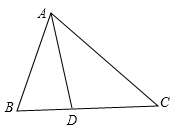
(1)若AC=BC,∠B:∠C=2:1,写出图中的所有等腰三角形,并给予证明;
(2)若AB+BD=AC,求∠B:∠C的比值.
已知一个等腰三角形的三边长分别为x,2x,5x-3,求这个三角形的周长.
请判断下列命题的真假性,若是假命题请举反例说明.
(1)若a>b,则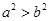 ;
;
(2)两个无理数的和仍是无理数;
(3)若三角形三边a,b,c满足(a-b)(b-c)(c-a)=0,则三角形是等边三角形;
(4)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形.
如图 ,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.求证:AC是BD的中垂线.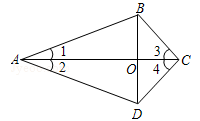
如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF.求证:点F在∠BAC的平分线上.