已知
(1)求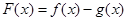 的极值,
的极值,
并证明:若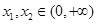 有
有 ;
;
(2)设 ,且
,且 ,
,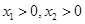 ,
,
证明: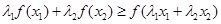 ,
,
若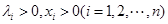 ,由上述结论猜想一个一般性结论(不需要证明);
,由上述结论猜想一个一般性结论(不需要证明);
(3)证明:若 ,则
,则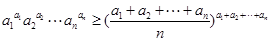
(本小题满分12分)
数列 满足
满足
(1)设 ,求证
,求证 是等比数列;(2) 求数列
是等比数列;(2) 求数列 的通项公式;
的通项公式;
(3)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
(本小题满分12分)
如图:某观测站 在城
在城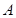 的南偏西
的南偏西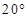 的方向上,从城
的方向上,从城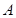 出发有一条走向为南偏东
出发有一条走向为南偏东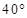 的公路,在
的公路,在 处测得距离
处测得距离 处
处 的公路上的
的公路上的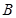 处有一辆车正沿着公路向城
处有一辆车正沿着公路向城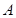 驶去,行驶了
驶去,行驶了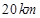 后到达
后到达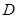 处,测得
处,测得 两处间的距离为
两处间的距离为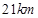 ,此时该车距城
,此时该车距城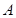 有多远?
有多远?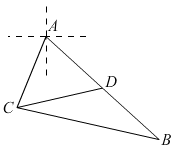
(本小题满分12分)
已知数列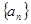 中,
中,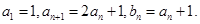
(1)证明:数列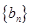 是等比数列;
是等比数列;
(2)令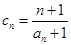 ,求数列
,求数列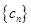 的前
的前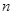 项和
项和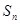

(本小题满分12分)
在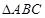 中,内角
中,内角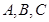 对边分别是
对边分别是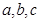 ,若
,若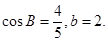
(1)当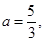 求角
求角 的度数;(2)求
的度数;(2)求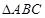 面积的最大值。
面积的最大值。
(本小题满分12分)
如下图,互相垂直的两条公路 、
、 旁有一矩形花园
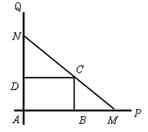
旁有一矩形花园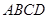 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园 ,要求点
,要求点 在射线
在射线 上,点
上,点 在射线
在射线 上,且直线
上,且直线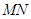 过点
过点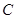 ,其中
,其中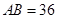 米,
米, 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为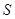 .
.
(Ⅰ)问: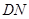 取何值时,
取何值时,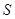 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(Ⅱ)若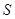 不超过1764平方米,求
不超过1764平方米,求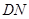 长的取值范围.
长的取值范围.