如图所示,四面体ABCD中,AB⊥BD、AC⊥CD且AD =3.BD=CD=2.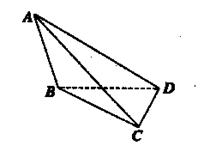
(1)求证:AD⊥BC;
(2)求二面角B—AC—D的余弦值.
已知等差数列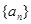 满足:
满足: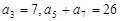 ,
,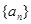 的前n项和为
的前n项和为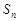 .
.
(1)求 及
及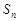 ;
;
(2)令 ,求数列
,求数列 的前n项和
的前n项和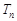 .
.
已知函数
⑴求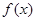 的最小正周期及对称中心;
的最小正周期及对称中心;
⑵若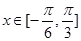 ,求
,求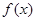 的最大值和最小值.
的最大值和最小值.
设函数 ,数列
,数列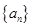 满足
满足 .
.
⑴求数列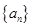 的通项公式;
的通项公式;
⑵设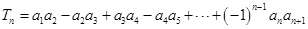 ,若
,若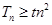 对
对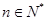 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
⑶是否存在以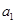 为首项,公比为
为首项,公比为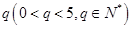 的数列
的数列 ,
,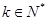 ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列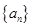 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.
已知函数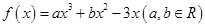 在点
在点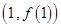 处的切线方程为
处的切线方程为 .
.
⑴求函数 的解析式;
的解析式;
⑵若对于区间 上任意两个自变量的值
上任意两个自变量的值 都有
都有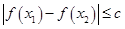 ,求实数
,求实数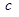 的最小值;
的最小值;
⑶若过点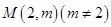 可作曲线
可作曲线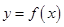 的三条切线,求实数
的三条切线,求实数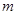 的取值范围.
的取值范围.
扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为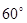 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为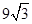 平方米,且高度不低于
平方米,且高度不低于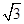 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为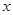 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段 与两腰长的和)为
与两腰长的和)为 (米).
(米).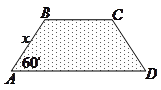
⑴求 关于
关于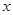 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过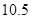 米,则其腰长
米,则其腰长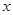 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长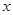 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.