为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
| 登记所需时间 |
1 |
2 |
3 |
4 |
5 |
| 频率 |
0.1 |
0.4 |
0.3 |
0.1 |
0.1 |
从第—个车主开始预约登记时计时(用频率估计概率),
(l)估计第三个车主恰好等待4分钟开始登记的概率:
(2)X表示至第2分钟末已登记完的车主人数,求X的分布列及数学期望.
(本小题满分14分)如图,在正三棱柱 中,
中,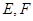 分别为
分别为 中点.
中点.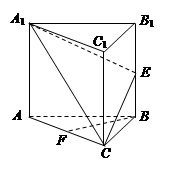
(1)求证: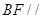 平面
平面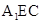 ;
;
(2)求证:平面 平面
平面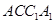 .
.
(本小题满分14分)如图,已知点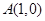 ,
,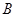 是单位圆
是单位圆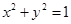 上一动点,且点
上一动点,且点 是线段
是线段 的中点.
的中点.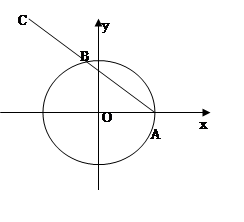
(1)若点 在
在 轴的正半轴上,求
轴的正半轴上,求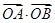 ;
;
(2)若 ,求点
,求点 到直线
到直线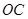 的距离.
的距离.
在直角坐标系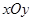 中,以坐标原点为极点,
中,以坐标原点为极点,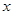 轴正半轴为极轴建立极坐标系,半圆
轴正半轴为极轴建立极坐标系,半圆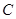 的极坐标方程为
的极坐标方程为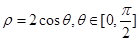 .
.
(1)求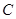 得参数方程;
得参数方程;
(2)设点 在
在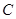 上,
上,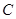 在
在 处的切线与直线
处的切线与直线 垂直,根据(1)中你得到的参数方程,确定
垂直,根据(1)中你得到的参数方程,确定 的坐标.
的坐标.
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线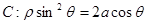
 ,已知过点
,已知过点 的直线
的直线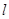 的参数方程为:
的参数方程为: ,直线
,直线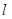 与曲线C分别交于
与曲线C分别交于 ;
;
(Ⅰ)写出曲线C参数方程和直线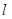 的普通方程;
的普通方程;
(Ⅱ)若 成等比数列,求
成等比数列,求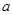 的值.
的值.
在直角坐标 中,圆
中,圆 ,圆
,圆 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆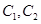 的极坐标方程,并求出圆
的极坐标方程,并求出圆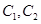 的交点极坐标(用极坐标表示);
的交点极坐标(用极坐标表示);
(Ⅱ)求圆 的公共弦的参数方程。
的公共弦的参数方程。