为了鼓励居民节约用水，我市某地水费按下表规定收取：
| 每户每月用水量 |
不超过10吨（含10吨） |
超过10吨的部分 |
| 水费单价 |
1.30元/吨 |
2.00元/吨 |
（1）某用户用水量为x吨，需付水费为y元，则水费y（元）与用水量x（吨）之间的函数关系式是
；
（2）若小华家四月份付水费17元，问他家四月份用水多少吨？
（3）已知某住宅小区100户居民五月份交水费1682元，且该月每户用水量均不超过15吨（含15吨），求该月用水量不超过10吨的居民最多可能有多少户？
.已知盒子中有4个红球，2个白球，从中一次抓三个球
（1）求没有抓到白球的概率；
（2）记抓到球中的红球数为X ，求X的分布列和数学期望.
变换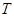
对应的变换矩阵是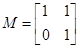
(1)求点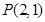
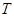在作用下的点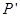
的坐标；
(2)求函数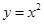
的图象在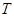变换的作用下所得曲线的方程.
已知函数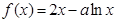
.
（1）求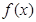
的单调递增区间；
（2）若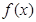在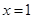
处的切线与直线
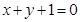垂直，求证：对任意
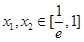，都有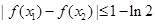
；
（3）若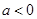
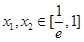，对于任意，都有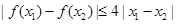
成立，求实数
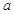的取值范围.
已知点P（4， 4），圆C：
与椭圆E：
有一个公共点A（3，1），F1、F2分别是椭圆的左、右焦点，直线PF1与圆C相切．
（Ⅰ）求m的值与椭圆E的方程；（Ⅱ）设Q为椭圆E上的一个动点，求
的取值范围．
已知椭圆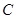
：
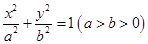的离心率为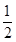
，
分别为椭圆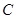的左、右焦点，若椭圆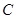的焦距为2．
⑴求椭圆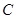的方程；
⑵设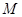
为椭圆上任意一点，以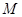为圆心，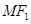
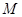为半径作圆，当圆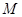与椭圆的右准线
有公共点时，求△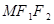
面积的最大值．