已知：如图，矩形ABCD，AB4，∠ACB30°．点E从点C-优题课

已知：如图，矩形ABCD，AB = 4，∠ACB = 30°．点E从点C出发，沿折线CA—AD以每秒一个单位长度的速度运动，过点E作EF∥CD交BC于点F，同时过点E作EG⊥AC交直线BC于点G，设运动的时间为t，△EFG与△ABC重叠部分的面积为S，当点E运动到点D时停止运动．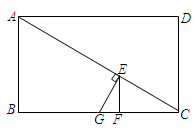

（1）当点B与点G重合时，求此时t的值；
（2）直接写出S与t之间的函数关系式和相应的自变量取值范围；
（3）当t = 4时，将△EFG绕点E顺时针旋转一个角度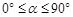（），∠GEF的两边分别交矩形的边于点M，点N．当△MEN为等腰三角形时，求此时△MEN的面积．

科目数学题型解答题难度中等

知识点：圆内接四边形的性质二次函数在给定区间上的最值

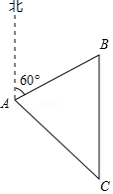
一艘渔船从位于 $A$ 海岛北偏东 $60 °$ 方向，距 $A$ 海岛60海里的 $B$ 处出发，以每小时30海里的速度沿正南方向航行．已知在 $A$ 海岛周围50海里水域内有暗礁．（参考数据： $\sqrt{3} \approx 1.73$ ， $\sqrt{5} \approx 2.24$ ， $\sqrt{7} \approx 2.65)$

（1）这艘渔船在航行过程中是否有触礁的危险？请说明理由．

（2）渔船航行3小时后到达 $C$ 处，求 $A$ ， $C$ 之间的距离．

今年6月份，永州市某中学开展"六城同创"知识竞赛活动．赛后，随机抽取了部分参赛学生的成绩，按得分划为 $A$ ， $B$ ， $C$ ， $D$ 四个等级， $A : 90 < S ⩽ 100$ ， $B : 80 < S ⩽ 90$ ， $C : 70 < S ⩽ 80$ ， $D : S ⩽ 70$ ．并绘制了如图两幅不完整的统计图，请结合图中所给信息，答案下列问题：

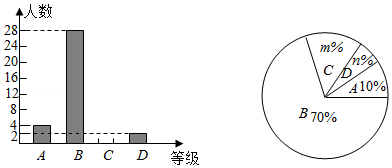
（1）请把条形统计图补充完整．

（2）扇形统计图中 $m =$ 　　， $n =$ 　　， $B$ 等级所占扇形的圆心角度数为　　．

（3）该校准备从上述获得 $A$ 等级的四名学生中选取两人参加永州市举行的"六城同创"知识竞赛，已知这四人中有两名男生（用 $A_{1}$ ， $A_{2}$ 表示），两名女生（用 $B_{1}$ ， $B_{2}$ 表示），请利用树状图法或列表法，求恰好抽到1名男生和1名女生的概率．

先化简，再求值： $(\frac{1}{a + 1} - \frac{a + 2}{a^{2} - 1} \cdot \frac{a^{2} - 2 a + 1}{a^{2} + 4 a + 4}) \cdot (a + 2)$ ，其中 $a = 2$ ．

计算： $2020^{0} + \sqrt[3]{8} \sin 30 ° - {(\frac{1}{2})}^{- 1}$ ．

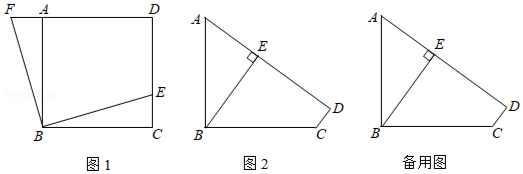
定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为"直角等邻对补"四边形，简称"直等补"四边形．

根据以上定义，解决下列问题：

（1）如图1，正方形 $ABCD$ 中， $E$ 是 $CD$ 上的点，将 $ΔBCE$ 绕 $B$ 点旋转，使 $BC$ 与 $BA$ 重合，此时点 $E$ 的对应点 $F$ 在 $DA$ 的延长线上，则四边形 $BEDF$ 为"直等补"四边形，为什么？

（2）如图2，已知四边形 $ABCD$ 是"直等补"四边形， $AB = BC = 5$ ， $CD = 1$ ， $AD > AB$ ，点 $B$ 到直线 $AD$ 的距离为 $BE$ ．

①求 $BE$ 的长；

②若 $M$ 、 $N$ 分别是 $AB$ 、 $AD$ 边上的动点，求 $ΔMNC$ 周长的最小值．

试卷网试题网古诗词网作文网范文网