如图，三棱锥
中，
是
的中点，
，
，
，
，二面角
的大小为
．
（1）证明：
平面
；
（2）求直线
与平面
所成角的正弦值．
解关于x的不等式
在四棱锥P－ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底 面ABCD是直角梯形，AB∥CD，∠ADC＝90°，AB＝AD＝PD＝1，CD＝2．
(Ⅰ)求证：BE∥平面PAD；
(Ⅱ)求证：BC⊥平面PBD；
(Ⅲ)求四棱锥P－ABCD的体积。
如图，直二面角A—BD—C，平面ABD⊥平面BCD,若其中给定 AB="AD" =2，
，
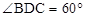，BC⊥CD .
（Ⅰ）求AC与平面BCD所成的角；
（Ⅱ）求点Ａ到BC的距离．
一个长、宽、高分别为a、b、c长方体的体积是8cm2，它的全面积是32 cm2，且满足 b2＝ac，求这个长方体所有棱长之和。
已知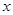
，
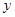满足约束条件
求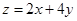
的最小值与最大值。