已知圆
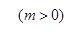 与抛物线
与抛物线 相交于
相交于 ,
, 两点
两点
(Ⅰ)求圆 的半径,抛物线的焦点坐标及准线方程;
的半径,抛物线的焦点坐标及准线方程;
(Ⅱ)设 是抛物线上不同于
是抛物线上不同于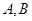 的点,且在圆外部,
的点,且在圆外部, 的延长线交圆于点
的延长线交圆于点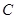 ,直线
,直线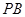 与
与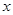 轴交于点
轴交于点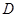 ,点
,点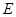 在直线
在直线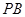 上,且四边形
上,且四边形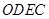 为等腰梯形,求点
为等腰梯形,求点 的坐标.
的坐标.
分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题:
(1)p: 是无理数,q:
是无理数,q:  大于是2
大于是2
(2)p: ,q:
,q:
(3)p:  , q:
, q: 
分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题:
(1)p:连续的三个整数的乘积能被2整除, q:连续的三个整数的乘积能被3整除.
(2)p:对角线互相垂直的四边形是菱形, q:对角线互相平分的四边形是菱形.
分别指出下列复合命题的形式及构成它的简单命题:
(1)3是质数或合数.
(2)他是运动员兼教练员.
(3)相似三角形不一定是全等三角形.
你能写出下列命题p的非(否定)吗?
(1)p:100既能被4整除又能被5整除
(2)p:三条直线两两相交
(3)p:一元二次方程至多有两个解
(4)p:
函数 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 . (1)判定函数
. (1)判定函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(2)问: 是
是 的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.