(本小题满分10分) 选修4—4：坐标系与参数方程.
已知曲线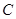
的参数方程为
（
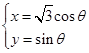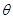为参数）,直线
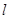的极坐标方程为
.
（1）写出曲线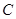的普通方程和直线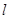的直角坐标方程;
（2）设点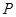
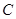为曲线上的动点,求点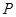到直线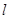距离的最大值.
已知动点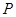
与双曲线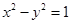
的两个焦点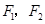
的距离之和为定值，且
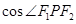的最小值为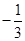
，求动点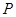的轨迹方程．
某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到一声巨响，正东观测点所到的时间比其他两个观测点晚期4s．已知各观测点到该中心的距离都是1020m．试确定该巨响发生的位置．（假定当时声音传播的速度为340m/s，相关各点均在同一平面上）．
已知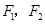
是双曲线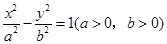
的左、右两焦点，过
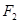作垂直于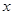
轴的直线交双曲线于点
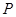，若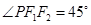
时，求双曲线的渐近线方程．
求中心在原点，对称轴为坐标轴，一个焦点是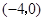
，一条渐近线是
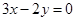的双曲线方程及离心率．
已知椭圆的焦点是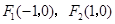
，
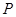为椭圆上一点，且
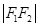是
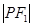和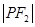
的等差中项．
（1）求椭圆的方程；
（2）若点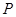在第三象限，且
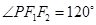，求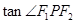
．