为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
①求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
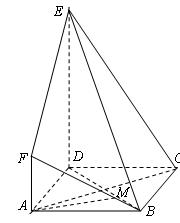
如图, 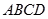 是边长为
是边长为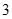 的正方形,
的正方形,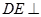 平面
平面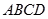 ,
,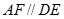 ,
,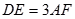 ,
,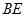 与平面
与平面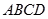 所成角为
所成角为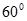 .
.
(Ⅰ)求证: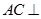 平面
平面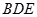 ;
;
(Ⅱ)求二面角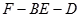 的余弦值;
的余弦值;
(Ⅲ)线段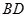 上是否存在点
上是否存在点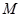 ,使得
,使得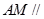 平面
平面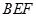 ?若存在,试确定点
?若存在,试确定点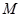 的位置;若不存在,说明理由。
的位置;若不存在,说明理由。
已知命题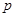 :
: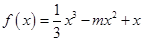 在
在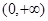 上是增函数;命题
上是增函数;命题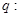 函数
函数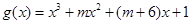 存在极大值和极小值。求使命题“
存在极大值和极小值。求使命题“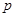 且
且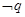 ”为真命题的
”为真命题的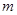 的取值范围。
的取值范围。
已知函数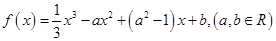 ,其图象在点
,其图象在点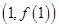 处的切线方程为
处的切线方程为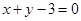
(1)求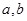 的值;
的值;
(2)求函数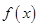 的单调区间,并求出
的单调区间,并求出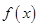 在区间[-2,4]上的最大值.
在区间[-2,4]上的最大值.
已知函数 ,
,  ,
, ,
, 、
、 .
.
(Ⅰ)若 ,判断
,判断 的奇偶性;
的奇偶性;
(Ⅱ) 若 ,
, 是偶函数,求
是偶函数,求 ;
;
(Ⅲ)是否存在 、
、 ,使得
,使得 是奇函数但不是偶函数?若存在,试确定
是奇函数但不是偶函数?若存在,试确定 与
与 的关系式;如果不存在,请说明理由.
的关系式;如果不存在,请说明理由.
已知向量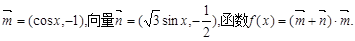
(Ⅰ)求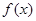 的最小正周期T;
的最小正周期T;
(Ⅱ)若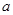 ,b,c分别为△ABC内角A,B,C的对边,A为锐角,
,b,c分别为△ABC内角A,B,C的对边,A为锐角, 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积.