如图所示,两根足够长的光滑金属导轨,相距为L=10cm,竖直放置,导轨上端连接着电阻R1=1Ω,质量为m=0.01kg,电阻为R2=0.2Ω的金属杆ab与导轨垂直并接触良好,导轨电阻不计.整个装置处于与导轨平面垂直的磁感应强度为B=1T的匀强磁场中.ab杆由静止释放,经过一段时间后达到最大速率,g取10m/s2,求此时:
(1)杆的速率; (2)ab间的电压; (3)电阻R1消耗的电功率.
如图所示,一定质量的理想气体从状态A变化到状态B,再由状态B变化到状态C.已知状态A的温度为300 K。气体在状态B的温度TB= ;由状态B变化到状态C的过程中,气体是 (吸热或放热)。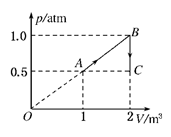
如图甲所示,水平传送A、B两轮间的距离L="3.0" m,质量M="1.0" kg可视为质点的物块随传送带一起以恒定的速率v0向左匀速运动,当物块运动到最左端时,质量m=0.020kg的子弹以u0=400m/s的水平速度向右射中物块并穿出。在传送带的右端有一传感器,测出物块被击穿后的速度随时间的变化关系如图乙所示(图中取向右运动的方向为正方向,子弹射出物块的瞬间为t=0时刻)。子弹击穿物块的时间可忽略不计,且子弹不会击中传感器,物块的质量不因被子弹击穿而发生改变。不计空气阻力及A、B轮的大小,g=10m/s2。求:
(1)物块与传送带间的动摩擦因数m;
(2)第一颗子弹击穿物块后到物块与传送带相对静止期间,物块与传送带间相对运动的总路程;
(3)如果从第一颗子弹击中物块开始,每隔Dt="1.5" s就有一颗相同的子弹以同样的速度击穿物块,所有子弹与物块间的相互作用力均相同,直至物块最终离开传送带,整个过程中物块与传动带之间因摩擦而产生的热量Q。
如图所示,光滑水平面上有正方形线框abcd,边长为L、电阻为R、质量为m。虚线PP′和QQ′之间有一竖直向上的匀强磁场,磁感应强度为B,宽度为H,且H>L。线框在恒力F0作用下开始向磁场区域运动,cd边运动S后进入磁场,ab边进入磁场前某时刻,线框已经达到平衡状态。当cd边开始离开磁场时,撤去恒力F0,重新施加外力F,使得线框做加速度大小为F0/m的匀减速运动,最终离开磁场。求:
(1)cd边刚进入磁场时两端的电势差Udc;
(2)cd边从进入磁场到运动至QQ′过程中安培力做功;
(3)写出线框离开磁场的过程中,F随时间t变化的关系式。
如图所示,光滑水平面上有正方形线框abcd,边长为L、电阻为R、质量为m。虚线PP′和QQ′之间有一竖直向上的匀强磁场,磁感应强度为B,宽度为H,且H>L。线框在恒力F0作用下开始向磁场区域运动,cd边运动S后进入磁场,ab边进入磁场前某时刻,线框已经达到平衡状态。当cd边开始离开磁场时,撤去恒力F0,重新施加外力F,使得线框做加速度大小为F0/m的匀减速运动,最终离开磁场。求:
(1)cd边刚进入磁场时两端的电势差Udc;
(2)cd边从进入磁场到运动至QQ′过程中安培力做功;
(3)写出线框离开磁场的过程中,F随时间t变化的关系式。
如图所示为一个自动控制装置的工作原理简图。在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω。在以O为圆心,半径为R=10 cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T。竖直平行放置的两金属板A、K相距为d,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H。比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上。离子进入电场的初速度、重力、离子之间的作用力均可忽略不计。问:
cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T。竖直平行放置的两金属板A、K相距为d,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H。比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上。离子进入电场的初速度、重力、离子之间的作用力均可忽略不计。问:
(1)判断离子的电性,并分段描述离子自S1到荧光屏D的运动情况?
(2)如果离子恰好垂直打在荧光屏上的N点,电压表的示数多大?
(3)电压表的最小示数是多少?要使离子打在荧光屏N点的右侧,可以采取哪些方法?