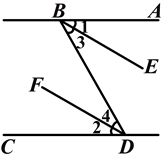已知:直线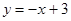 交
交 轴于点
轴于点 ,交
,交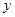 轴于点
轴于点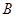 ,抛物线
,抛物线 经过
经过 、
、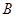 、
、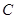 (1,0)三点.
(1,0)三点.
(1)求抛物线的解析式;
(2)若点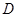 的坐标为(-1,0),在直线
的坐标为(-1,0),在直线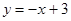 上有一点
上有一点 ,使
,使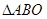 与
与 相似,求出点
相似,求出点 的坐标;
的坐标;
(3)在(2)的条件下,在 轴下方的抛物线上,是否存在点
轴下方的抛物线上,是否存在点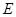 ,使
,使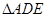 的面积等于四边形
的面积等于四边形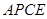 的面积?如果存在,请求出点
的面积?如果存在,请求出点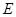 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
如图,AD∥BC,EF∥AD,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.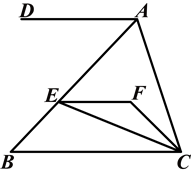
如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和点D,在直线CD上有一点P.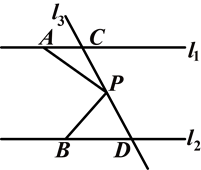
(1)如果P点在C、D之间运动,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由;
(2)若点P在C、D两点的外侧运动(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何.
实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=________°,∠3=________°.
(2)在(1)中,若∠1=55°,则∠3=________°;若∠1=40°,则∠3=________°.
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=________°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?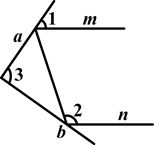
已知以下基本事实:①对顶角相等;②一条直线截两条平行直线所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线平行.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有________(填入序号即可);
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”.
已知:如图,________.
求证:________________________.
证明:________________________.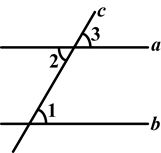
如图,AB∥CD,EB∥DF,试说明∠1=∠2.