已知数列 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意的
项和,对于任意的 ,满足关系式
,满足关系式
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的通项公式是
的通项公式是 ,前
,前 项和为
项和为 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有
设复数 ,试求m取何值时
,试求m取何值时
(1)Z是实数;(2)Z是纯虚数;(3)Z对应的点位于复平面的第一象限
定义在[-1,1]上的奇函数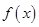 满足
满足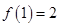 ,且当
,且当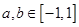 ,
, 时,有
时,有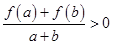 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若 对所有
对所有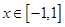 ,
,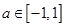 恒成立,
恒成立,
求实数m的取值范围.
海安县城有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动 小时的收费为
小时的收费为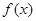 元
元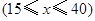 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动 小时的收费为
小时的收费为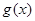 元
元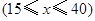 .试求
.试求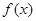 和
和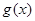 ;
;
(2)问:小张选择哪家比较合算?为什么?
)设 为奇函数,
为奇函数,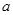 为常数.
为常数.
(1)求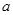 的值;
的值;
(2)判断 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;
(3)若对于区间 [3,4]上的每一个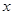 的值,不等式
的值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
二次函数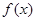 的图像顶点为
的图像顶点为 ,且图像在x轴上截得线段长为8
,且图像在x轴上截得线段长为8
(1)求函数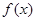 的解析式;
的解析式;
(2)令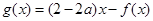
①若函数 在
在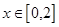 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围;
的取值范围;
②求函数 在
在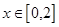 的最小值.
的最小值.