海安县城有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动 小时的收费为
小时的收费为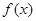 元
元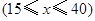 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动 小时的收费为
小时的收费为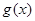 元
元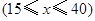 .试求
.试求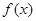 和
和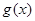 ;
;
(2)问:小张选择哪家比较合算?为什么?
数列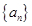 的前
的前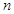 项和记为
项和记为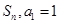 ,
,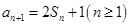
(Ⅰ)求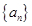 的通项公式;
的通项公式;
(Ⅱ)等差数列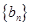 的各项为正,其前
的各项为正,其前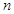 项和为
项和为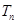 ,且
,且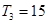 ,又
,又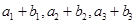 成等比数列,求
成等比数列,求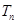 .
.
设函数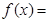
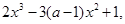 其中
其中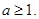
(Ⅰ)求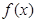 的单调区间;
的单调区间;
(Ⅱ) 讨论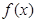 的极值.
的极值.
如右图,简单组合体ABCDPE,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
(1)若N为线段PB的中点,求证:EN⊥平面PDB;
(2)若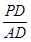 =
=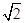 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.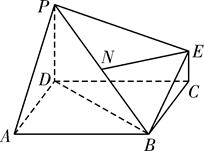
设△ABC的内角A,B,C所对的边长分别为a,b,c,m=(cosA,cosC),n=( c-2b,
c-2b, a)且m⊥n.
a)且m⊥n.
(1)求角A的大小;
(2)若角B= ,BC边上的中线AM的长为
,BC边上的中线AM的长为 ,求△ABC的面积.
,求△ABC的面积.
已知函数f(x)=-x3+3x2+9x+m
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.