已知函数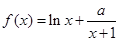 ,
,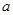 为常数.
为常数.
(1)若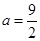 ,求函数
,求函数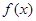 在
在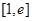 上的值域;(
上的值域;(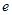 为自然对数的底数,
为自然对数的底数,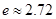 )
)
(2)若函数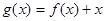 在
在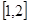 上为单调减函数,求实数
上为单调减函数,求实数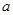 的取值范围.
的取值范围.
(本小题满分14分)已知函数 (
(  是自然对数的底数),
是自然对数的底数), .
.
(1)若 ,求
,求 的极值;
的极值;
(2)对任意 证明:
证明: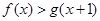 ;
;
(3)对任意 都有
都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知定点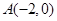 ,
,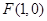 ,定直线
,定直线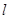 :
: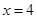 ,动点
,动点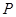 与点
与点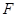 的距离是它到直线
的距离是它到直线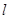 的距离的
的距离的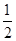 .设点
.设点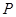 的轨迹为
的轨迹为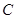 ,过点
,过点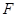 的直线交
的直线交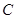 于
于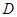 、
、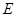 两点,直线
两点,直线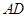 、
、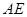 与直线
与直线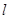 分别相交于
分别相交于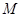 、
、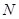 两点.
两点.
(1)求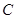 的方程;
的方程;
(2)以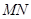 为直径的圆是否恒过一定点?若是,求出定点坐标;若不是,请说明理由.
为直径的圆是否恒过一定点?若是,求出定点坐标;若不是,请说明理由.
(本小题满分12分)已知数列 为等差数列,其中
为等差数列,其中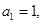
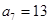 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列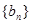 满足
满足 ,
,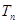 为数列
为数列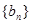 的前
的前 项和,当不等式
项和,当不等式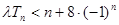 (
(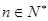 )恒成立时,求实数
)恒成立时,求实数 的取值范围.
的取值范围.
(本小题满分12分)如图,已知四边形ABCD为正方形,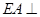 平面
平面 ,
, ∥
∥ ,且
,且
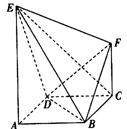
(1)求证: 平面
平面 ;
;
(2)求二面角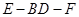 的余弦值.
的余弦值.
(本小题满分12分)
由于我市去年冬天多次出现重度污染天气,市政府决定从今年3月份开始进行汽车尾气的整治,为降低汽车尾气的排放量,我市某厂生产了甲、乙两种不同型号的节排器,分别从两种节排器中随机抽取100件进行性能质量评估检测,综合得分情况的频率分布直方图如图所示.
节排器等级如表格所示
| 综合得分K的范围 |
节排器等级 |
 |
一级品 |
 |
二级品 |
 |
三级品 |
若把频率分布直方图中的频率视为概率,则
(1)如果从甲型号中按节排器等级用分层抽样的方法抽取10件,然后从这10件中随机抽取3件,求至少有2件一级品的概率;
(2)如果从乙型号的节排器中随机抽取3件,求其二级品数 的分布列及数学期望.
的分布列及数学期望.