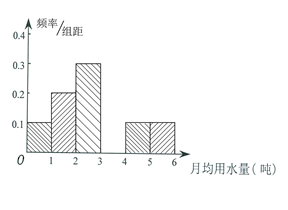
某市为节约用水,计划在本市试行居民生活用水定额管理,为了较为合理地确定居民日常用水量的标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),右表是100位居民月均用水量的频率分布表,根据右表解答下列问题:
| 分组 |
频数 |
频率 |
| [0,1) |
10 |
0.10 |
| [1,2) |
 |
0.20 |
| [2,3) |
30 |
0.30 |
| [3,4) |
20 |
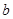 |
| [4,5) |
10 |
0.10 |
| [5,6] |
10 |
0.10 |
| 合计 |
100 |
1.00 |
(1)求右表中 和
和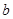 的值;
的值;
(2)请将频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.
设椭圆C: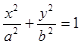
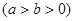 过点
过点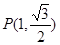 , 且离心率
, 且离心率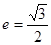 .
.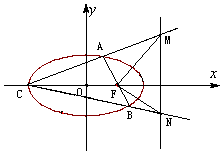
(Ⅰ)求椭圆C的方程;
(Ⅱ)过右焦点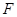 的动直线交椭圆于点
的动直线交椭圆于点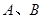 ,设椭圆的左顶点为
,设椭圆的左顶点为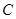 连接
连接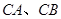 且交动直线
且交动直线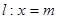 于
于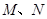 ,若以MN为直径的圆恒过右焦点F,求
,若以MN为直径的圆恒过右焦点F,求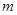 的值.
的值.
2011年4月28日世界园艺博览会将在陕西西安浐灞生态区举行,为了接待来自国内外的各界人士,需招募一批志愿者,要求志愿者不仅要有一定的气质,还需有丰富的人文、地理、历史等文化知识。志愿者的选拔分面试和知识问答两场,先是面试,面试通过后每人积60分,然后进入知识问答。知识问答有A,B,C,D四个题目,答题者必须按A,B,C,D顺序依次进行,答对A,B,C,D四题分别得20分、20分、40分、60分,每答错一道题扣20分,总得分在面试60分的基础上加或减。答题时每人总分达到100分或100分以上,直接录用不再继续答题;当四道题答完总分不足100分时不予录用。
假设志愿者甲面试已通过且第二轮对A,B,C,D四个题回答正确的概率依次是 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ) 用X表示志愿者甲在知识问答结束时答题的个数,求X的分布列和数学期望;
(Ⅱ)求志愿者甲能被录用的概率.
如图,在四边形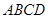 中,对角线
中,对角线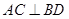 于
于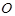 ,
,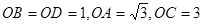 ,
,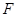 为
为 的重心,过点
的重心,过点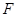 的直线
的直线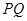 分别交
分别交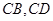 于
于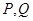 且
且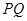 ‖
‖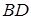 ,沿
,沿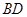 将
将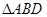 折起,沿
折起,沿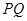 将
将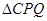 折起,
折起,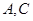 正好重合于
正好重合于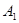 .
. 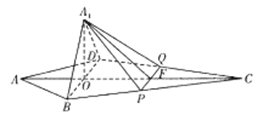
(Ⅰ) 求证:平面 平面
平面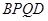 ;
;
(Ⅱ)求平面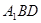 与平面
与平面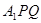 夹角的大小.
夹角的大小.
在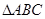 中,角
中,角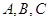 的对边分别为
的对边分别为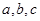 ,且向量
,且向量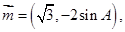
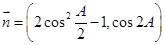 ,且
,且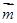 ‖
‖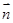 ,
,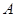 为锐角.
为锐角.
(Ⅰ)求角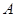 的大小;
的大小;
(Ⅱ)若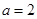 ,
, ,求
,求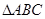 面积.
面积.
已知数列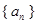 是首项为
是首项为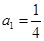 ,公比
,公比 的等比数列. 设
的等比数列. 设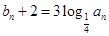
 ,数列
,数列 满足
满足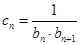 .
.
(Ⅰ)求证:数列 成等差数列;
成等差数列;
(Ⅱ)求数列 的前
的前 项和
项和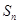 .
.