设椭圆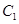 与抛物线
与抛物线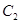 的焦点均在
的焦点均在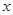 轴上,
轴上,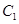 的中心及
的中心及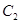 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
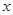 |
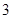 |
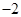 |
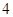 |
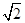 |
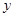 |
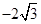 |
 |
 |
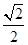 |
(Ⅰ)求曲线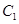 、
、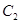 的标准方程;
的标准方程;
(Ⅱ)设直线 过抛物线
过抛物线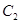 的焦点
的焦点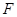 ,
,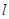 与椭圆交于不同的两点
与椭圆交于不同的两点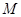 、
、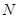 ,当
,当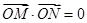 时,求直线
时,求直线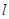 的方程.
的方程.
如图,等边 与直角梯形ABDE所在平面垂直,
与直角梯形ABDE所在平面垂直, ,AE⊥AB,
,AE⊥AB, ,O为AB的中点.
,O为AB的中点.
|

 ;
;
 的余弦值.
的余弦值.
在一次抗洪抢险中准备用射击的方法引爆从上游漂流而下的一个巨大汽油罐。已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆。每次射击是相互独立的,且命中的概率都是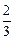 。
。
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光停止射击,设射击次数为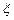 ,求
,求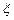 的分布列及数学期望。
的分布列及数学期望。
已知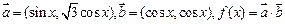 。(1)若
。(1)若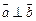 ,求
,求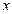 的取值集合;(2)求函数
的取值集合;(2)求函数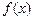 的周期及增区间。
的周期及增区间。
(本小题满分14分)
已知函数 ,
, ,且
,且
(Ⅰ)求函数的定义域,并证明 在定义域上是奇函数;
在定义域上是奇函数;
(Ⅱ)对于
 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅲ)当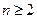 ,且
,且 时,试比较
时,试比较 与
与 的大小.
的大小.
(本小题满分14分)
已知椭圆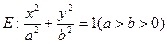 的左、右焦点分别为
的左、右焦点分别为 ,点
,点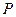 是
是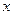 轴上方椭圆
轴上方椭圆 上的一点,且
上的一点,且 ,
,  ,
, 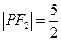 .
.
(Ⅰ) 求椭圆 的方程和
的方程和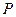 点的坐标;
点的坐标;
(Ⅱ)判断以 为直径的圆与以椭圆
为直径的圆与以椭圆 的长轴为直径的圆的位置关系;
的长轴为直径的圆的位置关系;
(Ⅲ)若点 是椭圆
是椭圆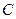 :
: 上的任意一点,
上的任意一点,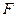 是椭圆
是椭圆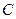 的一个焦点,探究以
的一个焦点,探究以 为直径的圆与以椭圆
为直径的圆与以椭圆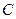 的长轴为直径的圆的位置关系.
的长轴为直径的圆的位置关系.