计算(每题 6分,共18分)
(1)2log525 + 3log264 (2)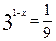 (3)
(3)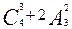 =
=
已知函数 ,曲线
,曲线 在
在 处的切线过点
处的切线过点 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)当 时,求
时,求 的取值范围.
的取值范围.
如图,直三棱柱 中,
中, ,
, ,D是AC的中点.
,D是AC的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求几何体 的体积.
的体积.
某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
 |
0.010 |
0.005 |
0.001 |
 |
6.635 |
7.879 |
10.828 |
附:
△ABC的内角A,B,C的对边分别为a,b,c,△ABC的面积 .
.
(Ⅰ)求C;
(Ⅱ)若a+b=2,且c= ,求A.
,求A.
已知 ,
, R
R
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)若 恒成立,求k的取值范围.
恒成立,求k的取值范围.