已知抛物线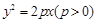 的焦点为
的焦点为 ,点
,点 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4, .
.
(1)求抛物线的方程;
(2)设点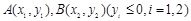 是抛物线上的两点,
是抛物线上的两点, 的角平分线与
的角平分线与 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;
(3)在(2)的条件下,若直线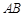 过点
过点 ,求弦
,求弦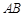 的长.
的长.
【原创】(1),已知: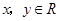 ,且满足
,且满足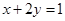 ,求
,求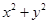 的最小值;
的最小值;
(2),已知: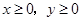 ,且满足
,且满足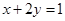 ,求
,求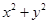 的最大值.
的最大值.
如图,正方形ABCD所在的平面与三角形CDE所在的平面交于CD,AE⊥平面CDE,且AB=2AE.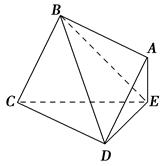
(1)求证:AB∥平面CDE;
(2)求证:平面ABCD⊥平面ADE.
光线从点A(2,3)射出,若镜面的位置在直线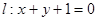 上,反射线经过 B(1,1),求入射光线和反射光线所在直线的方程,并求光线从A到B所走过的路线长
上,反射线经过 B(1,1),求入射光线和反射光线所在直线的方程,并求光线从A到B所走过的路线长
如图P、Q分别是A1B1、BB1的四等分点,M、N分别是D1C1、CC1的中点.沿M→N→Q→P截去一部分,截去的几何体是什么?剩下的几何体也是吗?
【原创】下面的一组图形为某一四棱锥S-ABCD的侧面与底面。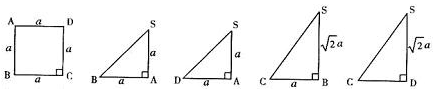
(1)请画出四棱锥S-ABCD的直观图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA 面ABCD,E为AB中点,求三棱锥
面ABCD,E为AB中点,求三棱锥 的体积;
的体积;
(3)求点D到面SEC的距离。