在平面直角坐标系中,已知点 及直线
及直线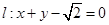 ,曲线
,曲线 是满足下列两个条件的动点
是满足下列两个条件的动点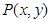 的轨迹:①
的轨迹:①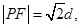 其中
其中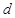 是
是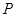 到直线
到直线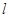 的距离;②
的距离;②
(1) 求曲线 的方程;
的方程;
(2) 若存在直线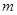 与曲线
与曲线 、椭圆
、椭圆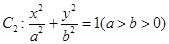 均相切于同一点,求椭圆
均相切于同一点,求椭圆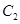 离心率
离心率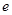 的取值范围.
的取值范围.
如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
已知数列{an}的前n项和为Sn,且满足Sn=n2,数列{bn}满足bn= ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.
(1)求数列{an}的通项公式an和Tn;
(2)若对任意的n∈N*,不等式λTn<n+(-1)n恒成立,求实数λ的取值范围.
已知函数f(x)= 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
已知等差数列{an}满足:a2=5,a4+a6=22,数列{bn}满足b1+2b2+…
+2n-1bn=nan,设数列{bn}的前n项和为Sn.
(1)求数列{an},{bn}的通项公式;
(2)求满足13<Sn<14的n的集合.
已知数列{an}的前n项和是Sn,且Sn+ an=1.
an=1.
(1)求数列{an}的通项公式;
(2)记bn=log3 ,数列
,数列 的前n项和为Tn,证明:Tn<
的前n项和为Tn,证明:Tn< .
.