已知等差数列{an}满足:a2=5,a4+a6=22,数列{bn}满足b1+2b2+…
+2n-1bn=nan,设数列{bn}的前n项和为Sn.
(1)求数列{an},{bn}的通项公式;
(2)求满足13<Sn<14的n的集合.
(本小题满分13分)
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从10个样本中随机抽出2名学生的成绩,设选出学生的分数为90分以上的人数为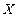 ,求随机变量
,求随机变量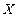 的分布列和均值.
的分布列和均值.
| 9 |
2 |
8 |
8 |
| 8 |
5 |
5 |
|
| 7 |
4 |
4 |
4 |
| 6 |
0 |
0 |
(本小题满分13分)
已知函数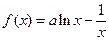 ,
,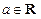 .
.
(Ⅰ)若曲线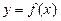 在点
在点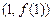 处的切线与直线
处的切线与直线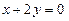 垂直,求
垂直,求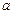 的值;
的值;
(Ⅱ)求函数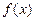 的单调区间;
的单调区间;
(Ⅲ)当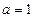 ,且
,且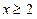 时,证明:
时,证明: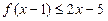 .
.
(本小题满分13分)
已知椭圆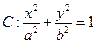
 的离心率为
的离心率为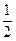 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线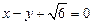 相切.
相切.
(Ⅰ)求椭圆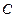 的方程;
的方程;
(Ⅱ)设 ,
,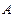 ,
,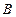 是椭圆
是椭圆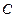 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆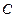 于另一点
于另一点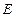 ,证明直线
,证明直线 与
与 轴相交于定点
轴相交于定点 ;
;
(Ⅲ)在(Ⅱ)的条件下,过点 的直线与椭圆
的直线与椭圆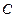 交于
交于 ,
,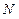 两点,求
两点,求 的取值范围.
的取值范围.
已知函数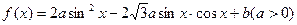 的定义域为
的定义域为 ,值域为
,值域为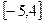 。试求函数
。试求函数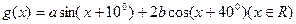
 的最小正周期T和最值。
的最小正周期T和最值。
已知函数
(1)设 为何值时,函数y取得最小值;
为何值时,函数y取得最小值;
(2)若函数y的最小值为1,试求a的值.