(本小题满分13分)
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从10个样本中随机抽出2名学生的成绩,设选出学生的分数为90分以上的人数为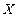 ,求随机变量
,求随机变量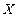 的分布列和均值.
的分布列和均值.
| 9 |
2 |
8 |
8 |
| 8 |
5 |
5 |
|
| 7 |
4 |
4 |
4 |
| 6 |
0 |
0 |
|
(本小题满分16分)
若曲线C: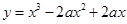 上任意点处的切线的倾斜角都为锐角,且a为整数。
上任意点处的切线的倾斜角都为锐角,且a为整数。
(1)求曲线C的解析式;
(2)求过点(1,1)的曲线的切线方程。
(本小题满分15分)已知函数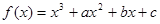 ,曲线
,曲线 在点
在点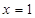 处的切线为
处的切线为 若
若 时,
时, 有极值.
有极值.
(1)求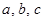 的值;
的值;
(2)求 在
在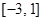 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)命题甲:“方程x2+mx+1=0有两个相异负根”,命题乙:“方程4x2+4(m-2)x+1=0无实根”,这两个命题有且只有一个成立,试求实数m的取值范围。
已知 是函数
是函数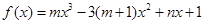 的一个极值点,其中
的一个极值点,其中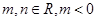 ,
,
(1)求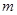 与
与 的关系式;
的关系式;
(2)求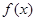 的单调区间;
的单调区间;
(3)当 时,函数
时,函数 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于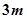 ,求
,求 的取值范围.
的取值范围.
已知函数 在
在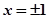 处取得极值。
处取得极值。
(1)讨论 和
和 是函数
是函数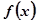 的极大值还是极小值.
的极大值还是极小值.
(2)求函数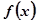 在
在 处的切线方程.
处的切线方程.
(3)求函数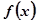 在区间
在区间 上的最值.
上的最值.