已知椭圆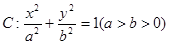 经过点
经过点 ,其离心率为
,其离心率为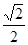 ,设直线
,设直线 与椭圆
与椭圆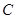 相交于
相交于 两点.
两点.
(Ⅰ)求椭圆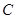 的方程;
的方程;
(Ⅱ)已知直线 与圆
与圆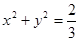 相切,求证:
相切,求证: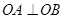 (
(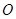 为坐标原点);
为坐标原点);
(Ⅲ)以线段 为邻边作平行四边形
为邻边作平行四边形 ,若点
,若点 在椭圆
在椭圆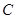 上,且满足
上,且满足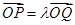 (
(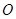 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围.
已知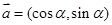 ,
,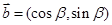 ,其中
,其中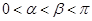
(1)求证: 与
与 互相垂直;
互相垂直;
(2)若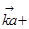
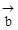 与
与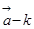
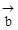 的长度相等,求
的长度相等,求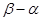 的值(
的值(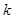 为非零的常数) .
为非零的常数) .
(1)若函数 ,则
,则 _______________.
_______________.
(2)化简: =____________.
=____________.
如图,ABCD是一块边长为100m的正方形地皮,其中AST是一半径为90m的扇形小山,其他部分都是平地.一开发商想在平地上建一个矩形停车场,使矩形的一个顶点P在弧ST上,相邻两边CQ,CR落在正方形的边BC,CD上,求矩形停车场PQCR的面积S的最大值和最小值(结果取整数).
)(如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0, 1),此时圆上一点P的位置在(0, 0),圆在x轴上沿正向滚动。当圆滚动到圆心位于(2, 1)时,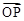 的坐标为______.
的坐标为______.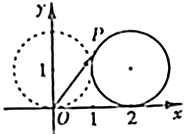
(2)在矩形ABCD中,边AB、AD的长分别为2、1,若M、N分别是边BC、CD上的点,且满足 ,则
,则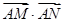 的取值范围是________.
的取值范围是________.
已知定义在实数集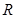 上的奇函数
上的奇函数 (
(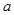 、
、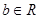 )过已知点
)过已知点 .
.
(Ⅰ)求函数的解析式;
(Ⅱ)试证明函数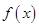 在区间
在区间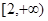 是增函数;若函数
是增函数;若函数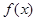 在区间
在区间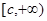 (其中
(其中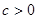 )也是增函数,求
)也是增函数,求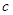 的最小值;
的最小值;
(Ⅲ)试讨论这个函数的单调性,并求它的最大值、最小值,在给出的坐标系(见答题卡)中画出能体现主要特征的图简;
(Ⅳ)求不等式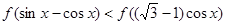 的解集.
的解集.