已知函数 ,其中
,其中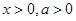
(Ⅰ)求函数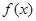 的定义域;
的定义域;
(Ⅱ)若对任意 恒有
恒有 ,试确定
,试确定 的取值范围.
的取值范围.
设函数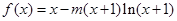 ,其中
,其中 为非负实数.
为非负实数.
(Ⅰ)求 的极大值;
的极大值;
(Ⅱ)当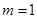 时,若直线
时,若直线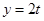 与函数
与函数 在
在 上的图象有交点,求实数
上的图象有交点,求实数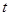 的取值范围;
的取值范围;
(Ⅲ)证明:当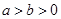 时,
时,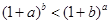 .
.
已知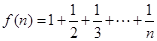 .经计算得
.经计算得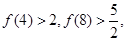
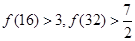 .
.
(Ⅰ)由上面数据,试猜想出一个一般性结论;
(Ⅱ)用数学归纳法证明你的猜想.
已知曲线 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.
(Ⅰ)求 解析式;
解析式;
(Ⅱ)求 的单调区间并画出
的单调区间并画出 的大致图象;
的大致图象;
(Ⅲ)已知函数 ,若对任意
,若对任意 ,总有
,总有
 求实数
求实数 的取值范围.
的取值范围.
某区要进行中学生篮球对抗赛,为争夺最后一个小组赛名额,甲、乙、丙三支篮球队要进行比赛,根据规则:每两支队伍之间都要比赛一场;每场比赛胜者得 分,负者得
分,负者得 分,没有平局,获得第一名的将夺得这个参赛名额.已知乙队胜丙队的概率为
分,没有平局,获得第一名的将夺得这个参赛名额.已知乙队胜丙队的概率为 ,甲队获得第一名的概率为
,甲队获得第一名的概率为 ,乙队获得第一名的概率为
,乙队获得第一名的概率为 .
.
(Ⅰ)求甲队分别战胜乙队和丙队的概率 ;
;
(Ⅱ)设在该次比赛中,甲队得分为 ,求
,求 的分布列及期望.
的分布列及期望.
已知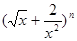 的展开式中,只有第六项的二项式系数最大.
的展开式中,只有第六项的二项式系数最大.
(Ⅰ)求该展开式中所有有理项的项数;
(Ⅱ)求该展开式中系数最大的项.