(1)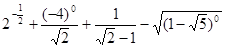
(2)求值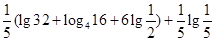
(本大题14分)
已知函数 定义域为
定义域为 ,且满足
,且满足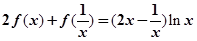 .
.
(Ⅰ)求 解析式及最小值;
解析式及最小值;
(Ⅱ)求证: ,
,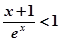 。
。
(Ⅲ)设 。求证:
。求证: ,
,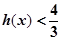 .
.
(本小题满分14分)
已知数列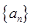 是公差不为零的等差数列,
是公差不为零的等差数列,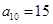 ,且
,且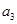 、
、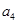 、
、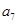 成等比数列.
成等比数列.
(Ⅰ)求数列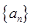 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为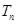 ,求证:
,求证:
(本小题满分13分)
已知空间向量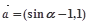 ,
, ,
, ·
· =
=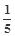 ,
,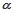 ∈(0,
∈(0,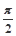 ).
).
(1)求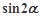 及
及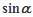 ,
, 的值;
的值;
(2)设函数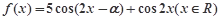 ,求
,求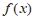 的最小正周期和图象的对称中心坐标;
的最小正周期和图象的对称中心坐标;
(3)求函数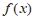 在区间
在区间 上的值域.
上的值域.
(本小题满分12分)
某出版社新出版一本高考复习用书,该书的成本为 元一本,经销过程中每本书需付给代理商
元一本,经销过程中每本书需付给代理商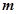 元
元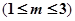 的劳务费,经出版社研究决定,新书投放市场后定价为
的劳务费,经出版社研究决定,新书投放市场后定价为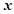 元一本,
元一本,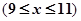 ,预计一年的销售量为
,预计一年的销售量为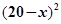 万本.
万本.
(Ⅰ)求该出版社一年的利润 (万元)与每本书的定价
(万元)与每本书的定价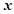 的函数关系式;
的函数关系式;
(Ⅱ)若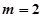 时,当每本书的定价为多少元时,该出版社一年利润
时,当每本书的定价为多少元时,该出版社一年利润 最大,并求出
最大,并求出 的最大值.
的最大值.