已知函数f(x)= 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
设圆 的极坐标方程为
的极坐标方程为 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为 轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆
轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆 上的一点
上的一点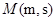 作平行于
作平行于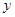 轴的直线
轴的直线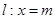 ,设
,设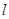 与
与 轴交于点
轴交于点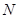 ,向量
,向量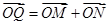 .
.
(Ⅰ)求动点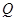 的轨迹方程;
的轨迹方程;
(Ⅱ)设点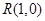 ,求
,求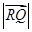 的最小值.
的最小值.
如图△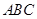 为直角三角形,
为直角三角形,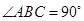 ,以
,以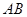 为直径的圆交
为直径的圆交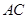 于点
于点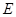 ,点
,点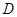 是
是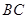 边的中点,连
边的中点,连 交圆
交圆 于点
于点 .
.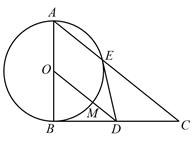
(Ⅰ)求证: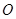 、
、 、
、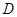 、
、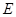 四点共圆;
四点共圆;
(Ⅱ)设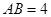 ,
, ,求
,求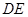 的长.
的长.
已知函数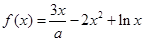
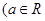 且
且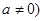 .
.
(Ⅰ)当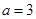 时,求在点
时,求在点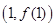 处的切线方程;
处的切线方程;
(Ⅱ)若函数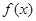 在区间
在区间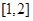 上为单调函数,求
上为单调函数,求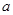 的取值范围.
的取值范围.
设椭圆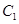 与抛物线
与抛物线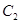 的焦点均在
的焦点均在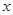 轴上,
轴上,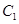 的中心及
的中心及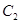 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
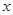 |
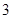 |
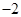 |
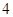 |
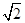 |
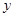 |
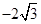 |
 |
 |
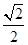 |
(Ⅰ)求曲线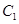 、
、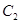 的标准方程;
的标准方程;
(Ⅱ)设直线 过抛物线
过抛物线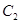 的焦点
的焦点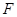 ,
,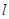 与椭圆交于不同的两点
与椭圆交于不同的两点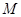 、
、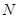 ,当
,当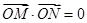 时,求直线
时,求直线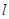 的方程.
的方程.
下表是我国2010年和2011年2~6月CPI同比(即当年某月与前一年同月相比)的增长数据,其中2011年的5个CPI数据成等差数列.
(Ⅰ)求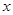 、
、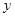 、
、 的值;
的值;
(Ⅱ)求2011年2~6月我国CPI数据的方差;
(Ⅲ)一般认为,某月CPI数据达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点为严重通货膨胀,现随机从2010年5个月和2011年5个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
我国2010年和2011年2~6月份的CPI数据(单位:百分点,1个百分点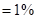 )
)
| 年份 |
二月 |
三月 |
四月 |
五月 |
六月 |
| 2010 |
2.7 |
2.4 |
2.8 |
3.1 |
3.9 |
| 2011 |
4.9 |
5.0 |
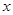 |
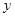 |
 |