下表是我国2010年和2011年2～6月CPI同比（即当年某月与前一年同月相比）的增长数据，其中2011年的5个CPI数据成等差数列.
（Ⅰ）求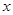
、
、
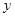的值；
（Ⅱ）求2011年2～6月我国CPI数据的方差；
（Ⅲ）一般认为，某月CPI数据达到或超过3个百分点就已经通货膨胀，而达到或超过5个百分点为严重通货膨胀，现随机从2010年5个月和2011年5个月的数据中各抽取一个数据，求相同月份2010年通货膨胀，并且2011年严重通货膨胀的概率.
我国2010年和2011年2～6月份的CPI数据（单位：百分点，1个百分点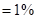
）
| 年份 |
二月 |
三月 |
四月 |
五月 |
六月 |
| 2010 |
2.7 |
2.4 |
2.8 |
3.1 |
3.9 |
| 2011 |
4.9 |
5.0 |
|
|
|
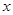已知函数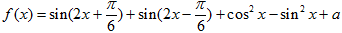
的在区间
上的最小值为0．
（Ⅰ）求常数a的值；
（Ⅱ）当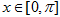
时，求使
成立的x的集合．
设函数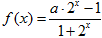
是实数集R上的奇函数．
（1）求实数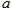
的值；
（2）判断
在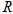
上的单调性并加以证明；
（3）求函数的值域．
设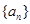
是公比为正数的等比数列，
，
．
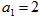（1）求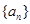的通项公式；
（2）设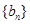
是首项为1，公差为2的等差数列，求数列
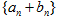的前
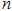项和
．
已知
各项均为正数的数列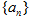
满足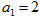
，
，
．
（1）求证：数列
是等比数列；
（2）当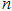
取何值时，
取最大值，并求出最大值；
（3）若
对任意
恒成立，求实数
的取值范围．
已知椭圆C：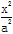
＋
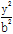＝1（a＞b＞0）的离心率为
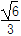，短轴一个端点到右焦点的距离为
．
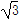（1）求椭圆C的方程；
（2）设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为
，求△AOB面积的最大值．