(本小题14分)如图所示,在四棱锥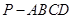 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 底面
底面 ,
, 为
为 的中点.
的中点.
(1)求直线 与
与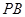 所成角的余弦值;
所成角的余弦值;
(2)在侧面 内找一点
内找一点 ,使
,使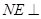 平面
平面 ,并分别求出点
,并分别求出点 到
到 和
和 的距离.
的距离.
(本小题14分)已知函数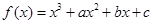 ,曲线
,曲线 在
在 处的切线方程为
处的切线方程为 ,若
,若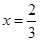 时,
时,  有极值.
有极值.
(1)求 的值; (2)求
的值; (2)求 在区间
在区间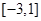 上的最大值和最小值.
上的最大值和最小值.
(本小题12分)试用含 的表达式表示
的表达式表示 的值,并用数学归纳法证明你的结论.
的值,并用数学归纳法证明你的结论.
(本小题12分) 设复数 (
( 是虚数单位), 试确定实数
是虚数单位), 试确定实数 ,使得:
,使得:
(1)  是纯虚数; (2)
是纯虚数; (2)  是实数; (3 )
是实数; (3 )  对应的点位于复平面的第二象限.
对应的点位于复平面的第二象限.
(本小题满分14分)已知函数 .
.
(1)试讨论函数 在
在 的单调性;
的单调性;
(2)若 ,求函数
,求函数 在
在 上的最大值和最小值;
上的最大值和最小值;
(3)若函数 在区间
在区间 上只有一个零点,求
上只有一个零点,求 的取值范围。
的取值范围。