盒子中装有四张大小形状均相同的卡片，卡片上分别标有数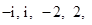
其中
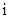是虚数单位．称“从盒中随机抽取一张，记下卡片上的数后并放回”为一次试验（设每次试验的结果互不影响）．
（1）求事件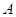
“在一次试验中，得到的数为虚数”的概率
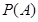与事件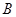
“在四次试验中，
至少有两次得到虚数” 的概率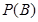
；
（2）在两次试验中，记两次得到的数分别为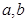
，求随机变量
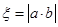的分布列与数学期望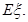
（本小题满分12分）如图，四棱锥P－ABCD的底面ABCD是直角梯形，∠DAB＝∠ABC＝90o，PA⊥底面ABCD，PA＝AB＝AD＝2，BC＝1，E为PD的中点．
(1) 求证：CE∥平面PAB；
(2) 求PA与平面ACE所成角的大小；
(3) 求二面角E－AC－D的大小．
(本小题满分12分) 设函数f(x）=
,其中向量
,
.
（1）求f（ 
）的值及f（ x）的最大值。
（2）求函数f（ x）的单调递增区间.
设曲线
：
上的点
到点
的距离的最小值为
,若
,
,
（1）求数列
的通项公式；
（2）求证:
；
（3）是否存在常数
,使得对
,都有不等式:
成立?请说明理由.
已知函数
，
R.
（1）求函数
的单调区间；
（2）是否存在实数
，使得函数的极值大于
？若存在，求的取值范围；若不存
在，说明理由.
已知向量
，
（1）求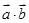
及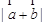
；
（2）若函数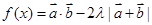
的最小值为
，求
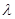的值.