(本小题满分12分) 设函数f(x)= ,其中向量
,其中向量
 ,
, .
.
(1)求f(  )的值及f( x)的最大值。
)的值及f( x)的最大值。
(2)求函数f( x)的单调递增区间.
对于函数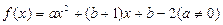 ,若存在实数
,若存在实数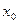 ,使
,使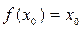 成立,则称
成立,则称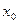 为
为 的不动点.
的不动点.
(1)当 时,求
时,求 的不动点;
的不动点;
(2)若对于任何实数 ,函数
,函数 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,若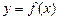 的图象上
的图象上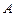 、
、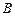 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线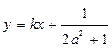 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的最小值.
的最小值.
已知点M(-2,0),N(2,0),动点P满足条件 ,该动点的轨迹为F,
,该动点的轨迹为F,
(1)求F的方程。
(2)若A、B是F上的不同两点,O是坐标原点,求 的最小值。
的最小值。
已知向量 =(cos
=(cos x,sin
x,sin x),
x), =(
=(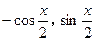 ),且x∈[0,
),且x∈[0, ].
].
(1)求 ;
;
(2)设函数 +
+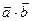 ,求函数
,求函数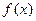 的最值及相应的
的最值及相应的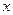 的值。
的值。
设数列 满足:
满足: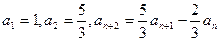 ,(n=1,2,…)。
,(n=1,2,…)。
(1)令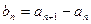 ,(n=1,2,…)。求数列
,(n=1,2,…)。求数列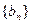 的通项公式;(2)求数列
的通项公式;(2)求数列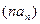 的前n项和Sn。
的前n项和Sn。
已知两点P1(4,9)和P2(6,3),求以P1P2为直径的圆的方程,并判断M(6,9),Q(5,3)是在圆上?圆外?圆内?