阅读解答：（1）填空：21202（）22212（）23222-优题课

阅读解答：
（1）填空：
2¹-2⁰=   =2^（^）
2²-2¹=   =2^（^）
2³-2²=   =2^（^）
………
（2）探索（1）中式子的规律，试写出第n个等式，并说明第n个等式成立。
（3）计算：2⁰+2¹+2²+2³+2⁴+…+2¹⁰⁰⁰

科目数学题型解答题难度中等

知识点：整式的加减

如图，一渔船自西向东追赶鱼群，在 $A$ 处测得某无名小岛 $C$ 在北偏东 $60 °$ 方向上，前进2海里到达 $B$ 点，此时测得无名小岛 $C$ 在东北方向上．已知无名小岛周围2.5海里内有暗礁，问渔船继续追赶鱼群有无触礁危险？（参考数据： $\sqrt{2} \approx 1.414, \sqrt{3} \approx 1.732)$

为满足市场需求，新生活超市在端午节前夕购进价格为3元 $/$ 个的某品牌粽子，根据市场预测，该品牌粽子每个售价4元时，每天能出售500个，并且售价每上涨0.1元，其销售量将减少10个，为了维护消费者利益，物价部门规定，该品牌粽子售价不能超过进价的 $200 %$ ，请你利用所学知识帮助超市给该品牌粽子定价，使超市每天的销售利润为800元．

如图，直线 $y = - \frac{1}{2} x + 1$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，抛物线 $y = - x^{2} + bx + c$ 经过 $A$ 、 $B$ 两点．

（1）求抛物线的解析式；

（2）点 $P$ 是第一象限抛物线上的一点，连接 $PA$ 、 $PB$ 、 $PO$ ，若 $ΔPOA$ 的面积是 $ΔPOB$ 面积的 $\frac{4}{3}$ 倍．

①求点 $P$ 的坐标；

②点 $Q$ 为抛物线对称轴上一点，请直接写出 $QP + QA$ 的最小值；

（3）点 $M$ 为直线 $AB$ 上的动点，点 $N$ 为抛物线上的动点，当以点 $O$ 、 $B$ 、 $M$ 、 $N$ 为顶点的四边形是平行四边形时，请直接写出点 $M$ 的坐标．

已知， $ΔABC$ 为直角三角形， $∠ ACB = 90 °$ ，点 $P$ 是射线 $CB$ 上一点（点 $P$ 不与点 $B$ 、 $C$ 重合），线段 $AP$ 绕点 $A$ 顺时针旋转 $90 °$ 得到线段 $AQ$ ，连接 $QB$ 交射线 $AC$ 于点 $M$ ．

（1）如图①，当 $AC = BC$ ，点 $P$ 在线段 $CB$ 上时，线段 $PB$ 、 $CM$ 的数量关系是　　；

（2）如图②，当 $AC = BC$ ，点 $P$ 在线段 $CB$ 的延长线时，（1）中的结论是否成立？若成立，写出证明过程；若不成立，请说明理由．

（3）如图③，若 $\frac{AC}{BC} = \frac{5}{2}$ ，点 $P$ 在线段 $CB$ 的延长线上， $CM = 2$ ， $AP = 13$ ，求 $ΔABP$ 的面积．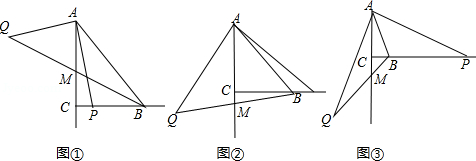

如图，某巡逻艇计划以40海里 $/$ 时的速度从 $A$ 处向正东方向的 $D$ 处航行，出发1.5小时到达 $B$ 处时，突然接到 $C$ 处的求救信号，于是巡逻艇立刻以60海里 $/$ 时的速度向北偏东 $30 °$ 方向的 $C$ 处航行，到达 $C$ 处后，测得 $A$ 处位于 $C$ 处的南偏西 $60 °$ 方向，解救后巡逻艇又沿南偏东 $45 °$ 方向航行到 $D$ 处．

（1）求巡逻艇从 $B$ 处到 $C$ 处用的时间．

（2）求巡逻艇实际比原计划多航行了多少海里？（结果精确到1海里）．

（参考数据： $\sqrt{3} \approx 1.73, \sqrt{6} \approx 2.45)$

试卷网试题网古诗词网作文网范文网