在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.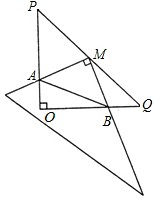
(1)求证:MA=MB;
(2)连接AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
联想中学本学期前三周每周都组织初三年级学生进行一次体育活动,全年级400名学生每人每次都只参加球类或田径类中一个项目的活动.假设每次参加球类活动的学生中,下次将有20%改为参加田径类活动;同时每次参加田径类活动的学生中,下次将有30%改为参加球类活动.
⑴如果第一次与第二次参加球类活动的学生人数相等,那么第一次参加球类活动的学生应有多少名?
⑵如果第三次参加球类活动的学生不少于200名,那么第一次参加球类活动的学生最少有多少名?
已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连结两条线段,如果你所连结的两条线段满足相等、垂直或平行关系中的一种,那么请你把它写出来并证明.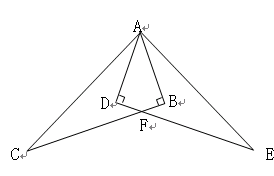
如图,在 ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠BAE=∠CDF.
ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠BAE=∠CDF.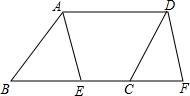
先化简再求值: ,其中
,其中
伟大的文学家、杰出的社会活动家高尔基说:“书籍,是人类进步的阶梯”,阅读使你增长知道,陶冶情操。李楠同学在课外阅读《三国演义》时,她将书翻到某一页,看完后往前翻了10页,然后她又往后翻了8页,这时她发现这三页的页码之和刚好是100,那么该书的这三页的页码分别是多少?