如图所示，在xOy平面的y轴左侧存在沿y轴正方向的匀强电场，y轴右侧区域Ⅰ内存在磁感应强度大小B1=mv0/ql面向外的匀强磁场，区域Ⅰ、区域Ⅱ的宽度均为L，高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为（– 2L，–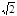
L）的A点以速度v0沿 +x方向射出，恰好经过坐标为[0，-(
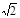–1)L]的C点射入区域Ⅰ。粒子重力忽略不计。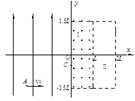
⑴ 求匀强电场的电场强度大小E；
⑵ 求粒子离开区域Ⅰ时的位置坐标；
⑶ 要使粒子从区域Ⅱ上边界离开磁场，可在区域Ⅱ内加垂直纸面向内的匀强磁场。试确定磁感应强度B的大小范围，并说明粒子离开区域Ⅱ时的速度方向。
如图甲所示，在两平行金属板的中线OO′某处放置一个粒子源，粒子沿OO1方向连续不断地放出速度
的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场，磁感应强度B=0.01
T，方向垂直纸面向里，MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比
，粒子的重力和粒子之间的作用力均可忽略不计，若
时刻粒子源放出的粒子恰能从平行金属板边缘离开电场（设在每个粒子通过电场区域的时间内，可以把板间的电场看作是恒定的）。求：
（1）时刻粒子源放出的粒子离开电场时的速度大小和方向。
（2）从粒子源放出的粒子在磁场中运动的最短时间和最长时间。
如图所示，水平面上有两电阻不计的光滑金属导轨平行固定放置，间距d为0.5 m，左端通过导线与阻值为2 W的电阻R连接，右端通过导线与阻值为4 W的小灯泡L连接，在CDEF矩形区域内有竖直向上的匀强磁场，CE长为2 m，CDEF区域内磁场的磁感应强度B随时间变化如图所示，在t＝0时，一阻值为2 W的金属棒在恒力F作用下由静止开始从ab位置沿导轨向右运动，当金属棒从ab位置运动到EF位置过程中，小灯泡的亮度没有发生变化，求：
（1）通过小灯泡的电流强度。
（2）恒力F的大小。
（3）金属棒的质量。
一个在地球上做简谐运动的单摆，其振动图象如左下图所示，今将此单摆移至某一行星上，其简谐运动图象如右下图所示.若已知该行星的质量为地球质量的2倍，求该行星的半径与地球半径之比.
如图所示，ABC和DEF是在同一竖直平面内的两条光滑轨道，其中ABC的末端水平，DEF是半径为r=0.4m的半圆形轨道，其直径DF沿竖直方向，C、D可看作重合．现有一质量为m=1kg可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放，
（1）若要使小球经C处水平进入轨道DEF且能沿轨道运动，H至少要有多高？
（2）若小球静止释放处离C点的高度h小于（1）中H的最小值，小球可击中与圆心等高的E点，求h．（取g=10m/s2）
（3）若小球自H=0.3m处静止释放,求小球到达F点对轨道的压力大小．
一架老式飞机在高出地面4.5km的高度，以1000／s的速度水平飞行。某时刻投下一颗炸弹，不计空气阻力
（1）求炸弹下落的时间？
（2）为了使飞机上投下的炸弹落在指定的目标上，应该在与轰炸目标的水平距离为多远的地方投弹?。