某高速公路收费站入口处的安全标识墩如图1所示。墩的上半部分是正四棱锥 ,下半部分是长方体
,下半部分是长方体 。图2、图3分别是该标识墩的正(主)视图和俯视图。
。图2、图3分别是该标识墩的正(主)视图和俯视图。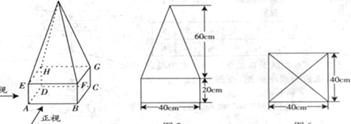
图1 图2 图3
(1)请在正视图右侧画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
如图,已知椭圆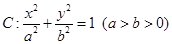 的左、右焦点分别为
的左、右焦点分别为 ,其上顶点为
,其上顶点为 已知
已知 是边长为
是边长为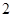 的正三角形.
的正三角形.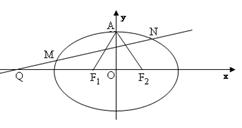
(1)求椭圆 的方程;
的方程;
(2)过点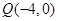 任作一动直线
任作一动直线 交椭圆
交椭圆 于
于 两点,记
两点,记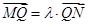 .若在线段
.若在线段 上取一点
上取一点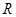 ,使得
,使得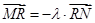 ,当直线
,当直线 运动时,点
运动时,点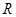 在某一定直线上运动,求出该定直线的方程.
在某一定直线上运动,求出该定直线的方程.
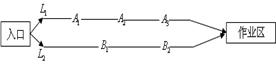
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有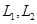 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图),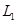 巷道有
巷道有 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是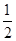 ;
; 巷道有
巷道有 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为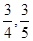 .
.
(1)求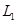 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若 巷道中堵塞点个数为
巷道中堵塞点个数为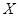 ,求
,求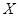 的分布列及数学期望
的分布列及数学期望 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
已知等差数列 的首项
的首项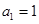 ,公差
,公差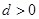 ,且第
,且第 项、第
项、第 项、第
项、第 项分别是等比数列
项分别是等比数列 的第
的第 项、第
项、第 项、第
项、第 项.
项.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)设数列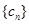 对
对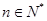 ,均有
,均有 成立,求
成立,求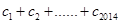 .
.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,点
,点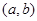 在直线
在直线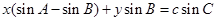 上.
上.
(1)求角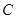 的值;
的值;
(2)若 ,且
,且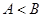 ,求
,求 .
.
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,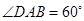 ,
,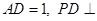 底面
底面
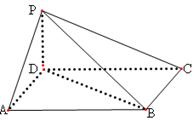
(1)证明: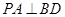 ;
;
(2)若 ,求二面角
,求二面角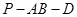 余弦值.
余弦值.