如图,A,B是海面上位于东西方向相距 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距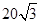 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?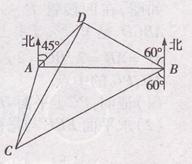
(本小题满分12分)
在△ABC中,设角A、B、C的对边分别为a、b、c,且 .
.
(1)求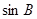 的值;
的值;
(2)若 ,且
,且 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分14分)
已知函数 在
在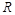 上有定义,对任意实数
上有定义,对任意实数 和任意实数
和任意实数 ,都有
,都有 .
.
(Ⅰ)证明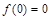 ;
;
(Ⅱ)证明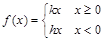 (其中k和h均为常数);
(其中k和h均为常数);
(Ⅲ)当(Ⅱ)中 的时,设
的时,设 ,讨论
,讨论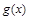 在
在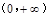 内的单调性.
内的单调性.
(本小题满分12分)
如图,在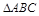 中,设
中,设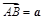 ,
, ,
, 的中点为
的中点为 ,
, 的中点为
的中点为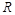 ,
, 的中点恰为
的中点恰为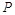 .
.
(Ⅰ)若 ,求
,求 和
和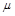 的值;
的值;
(Ⅱ)以 ,
,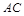 为邻边,
为邻边,  为对角线,作平行四边形
为对角线,作平行四边形 ,
,
求平行四边形 和三角形
和三角形 的面积之比
的面积之比 .
.
(本小题满分12分)
已知 的内角
的内角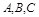 所对的边分别是
所对的边分别是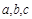 ,设向量
,设向量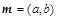 ,
,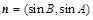 ,
, .
.
(Ⅰ)若 //
// ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(Ⅱ)若 ⊥
⊥ ,边长
,边长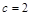 ,
, ,求
,求 的面积.
的面积.
(本小题满分13分)
已知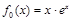 ,
,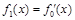 ,
,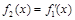 ,…,
,…,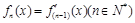 .
.
(Ⅰ)请写出的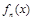 表达式(不需证明);
表达式(不需证明);
(Ⅱ)求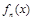 的极小值
的极小值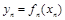 ;
;
(Ⅲ)设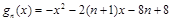 ,
,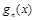 的最大值为
的最大值为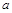 ,
,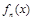 的最小值为
的最小值为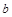 ,试求
,试求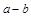 的最小值.
的最小值.