已知等差数列{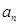 }中,
}中, =14,前10项和
=14,前10项和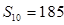 . (1)求
. (1)求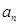 ;
;
(2)将{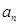 }中的第2项,第4项,…,第
}中的第2项,第4项,…,第 项按原来的顺序排成一个新数列{
项按原来的顺序排成一个新数列{ },令
},令 ,求数列{
,求数列{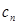 }的前
}的前 项和
项和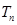 .
.
某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知函数 ,
, .
.
(1)求 的最小正周期;
的最小正周期;
(2)求 在闭区间
在闭区间 上的最大值和最小值.
上的最大值和最小值.
在数列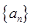 中,
中,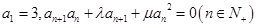 。
。
(1)若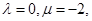 求数列
求数列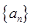 的通项公式;
的通项公式;
(2)若 证明:
证明: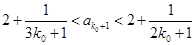 .
.
如图,设椭圆 的左.右焦点分别为
的左.右焦点分别为 ,点
,点 在椭圆上,
在椭圆上, ,
, ,
, 的面积为
的面积为 .
.
(1)求该椭圆的标准方程;
(2)设圆心在 轴上的圆与椭圆在
轴上的圆与椭圆在 轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径.
轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径.
已知函数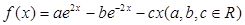 的导函数
的导函数 为偶函数,且曲线
为偶函数,且曲线 在点
在点 处的切线的斜率为
处的切线的斜率为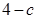 .
.
(1)确定 的值;
的值;
(2)若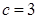 ,判断
,判断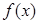 的单调性;
的单调性;
(3)若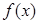 有极值,求
有极值,求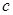 的取值范围.
的取值范围.