如图,已知AC⊥平面CDE,BD//AC,△ECD为等边三角形,F为ED边的中点,CD=BD=2AC=2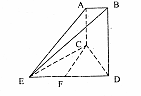
(1)求证:CF∥面ABE;
(2)求证:面ABE⊥平面BDE:
(3)求三棱锥F—ABE的体积。
(本小题满分12分)
已知函数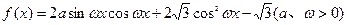 的最大值为2
的最大值为2 是集合
是集合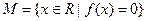 中的任意两个元素,
中的任意两个元素, 的最小值为
的最小值为 .
.
(Ⅰ)求 的值
的值
(Ⅱ)若 ,求
,求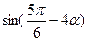 的值
的值
(本小题满分12分)(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答 只以甲题计分)
只以甲题计分)
甲:设数列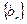 的前
的前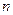 项和为
项和为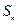 ,且
,且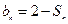 ;数列
;数列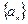 为等差数列,且
为等差数列,且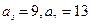
(Ⅰ)求数列 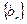 的通项公式
的通项公式
(Ⅱ)若 ,
,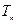 为数列
为数列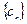 的前
的前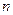
 项和,求
项和,求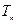
乙:定义在[-1,1]上的奇函数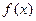 ,已知当
,已知当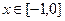 时,
时,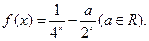
(Ⅰ)求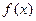 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若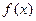 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数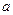 的取值范围
的取值范围
(本小题满分12分)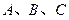 所对的边分别为
所对的边分别为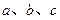 ,且
,且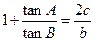 .
.
(Ⅰ)求角A;
(Ⅱ)已知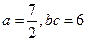 求
求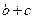 的值.
的值.
(本小题满分12分 )
)
已知集合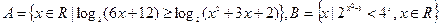 .
.
求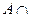 (CRB )
(CRB )
(本小题满分14分)设{an}是等差数列,{bn}是各项都为正数的等比数列,且
a1=b1=1,a3+b5=21,a5+b3=13.
(Ⅰ)求{an},{bn }的通项公式;
}的通项公式;
(Ⅱ)求数列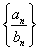 的前n项和
的前n项和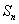 .
.