乳制品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5。现从一批该乳制品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
(1)若所抽取的20件乳制品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的乳制品记为 ,等级系数为5的乳制品记为
,等级系数为5的乳制品记为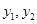 ,现从这5件乳制品
,现从这5件乳制品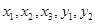 中任取两件(假定每件乳制品被取出的可能性相同),写出所有可能的结果,并求这两件乳制品的等级系数恰好相同的概率
中任取两件(假定每件乳制品被取出的可能性相同),写出所有可能的结果,并求这两件乳制品的等级系数恰好相同的概率
已知向量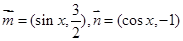 ,设
,设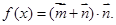
(1)求函数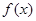 的表达式,并求
的表达式,并求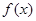 的单调递减区间;
的单调递减区间;
(2)在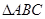 中,a,b,c分别是角A,B,C的对边,若
中,a,b,c分别是角A,B,C的对边,若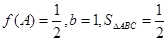 ,求a的值。
,求a的值。
已知函数
(I)求 的极小值;
的极小值;
(II)若 上为单调增函数,求m的取值范围;
上为单调增函数,求m的取值范围;
(III)设 (e是自然对数的底数)上至少存在一个
(e是自然对数的底数)上至少存在一个 成立,求m的取值范围。
成立,求m的取值范围。
设椭圆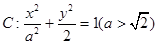 的左右焦点分别为F1,F2,A是椭圆C上第一象限内一点,
的左右焦点分别为F1,F2,A是椭圆C上第一象限内一点,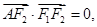 坐标原点O到直线AF1的距离为
坐标原点O到直线AF1的距离为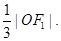
(I)求椭圆C的方程;
(II)设Q是椭圆C上的一点,过点Q的直线l交x轴于点 若
若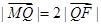 ,求直线l的斜率。
,求直线l的斜率。
若数列 ,其中T为正整数,则称数列
,其中T为正整数,则称数列 为周期数列,其中T为数列
为周期数列,其中T为数列 的周期。
的周期。
(I)设 是周期为7的数列,其中
是周期为7的数列,其中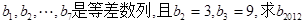 ;
;
(II)设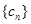 是周期为7的数列,其中
是周期为7的数列,其中 ,对(I)中的数列
,对(I)中的数列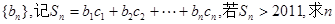 的最小值。
的最小值。