（本小题满分12分）为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：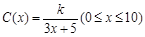
，若不建隔热层，每年能源消耗费用为8万元．设
为隔热层建造费用与20年的能源消耗费用之和．
（1）求
的值及的表达式；
（2）隔热层修建多厚时，总费用达到最小，并求最小值．
(本小题满分13分)
在一次数学考试中，共有10道选择题，每题均有四个选项，其中有且只有一个选项是正确的，评分标准规定：“每道题只选一个选项，答对得5分，不答或答错得零分”.某考生已确定有6道题是正确的，其余题目中：有两道题可判断两个选项是错误的，有一道可判断一个选项是错误的，还有一道因不理解题意只好乱猜，请求出该考生：
(Ⅰ)得50分的概率；
(Ⅱ)得40分的概率.
(本小题满分13分)
已知
为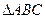
的三内角，且其对边分别为
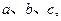若
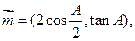
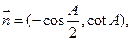且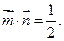
(Ⅰ)求角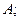
(Ⅱ)若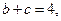
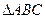的面积为
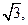求
(本小题满分12分)
设各项为正的数列
满足：
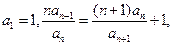令
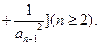
(Ⅰ)求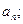
(Ⅱ)求证：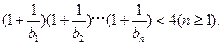
(本小题满分12分)
已知曲线
上任意一点
到点
的距离比它到直线
的距离小1.
(Ⅰ)求曲线的方程；
(Ⅱ)直线
与曲线相交于
两点，
设直线
的斜率分别为
求证：
为定值.
(本小题满分12分)
已知函数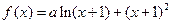
，其中，
为实常数且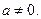
(Ⅰ)求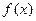
的单调增区间；
(Ⅱ)若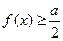
对任意
恒成立，求实数的取值范围.