选修4-5 不等式选讲
已知函数
(I)试求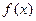 的值域;
的值域;
(II)设 ,若对
,若对 ,恒有
,恒有 成立,试求实数a的取值范围。
成立,试求实数a的取值范围。
选修4—4:坐标系与参数方程
在平面直角坐标系中,直线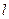 过点
过点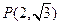 且倾斜角为
且倾斜角为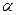 ,以坐标原点为极点,
,以坐标原点为极点,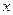 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线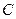 的极坐标方程为
的极坐标方程为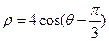 ,直线
,直线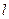 与曲线
与曲线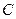 相交于
相交于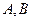 两点;
两点;
(1)若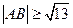 ,求直线
,求直线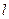 的倾斜角
的倾斜角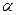 的取值范围;
的取值范围;
(2)求弦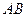 最短时直线
最短时直线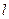 的参数方程。
的参数方程。
选做题(本小题满分10分,请考生在第22、23、24三题中任选一题作答。如果多做,则按所做的第一题计分,作答时请在答题纸上所选题目的方框内打“√”。
22.选修4-1:几何证明选讲。
如图,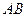 是圆
是圆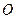 的直径,
的直径,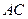 是弦,
是弦,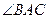 的平分线
的平分线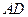 交圆
交圆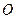 于点
于点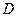 ,
,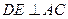 ,交
,交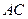 的延长线于点
的延长线于点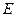 ,
,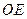 交
交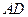 于点
于点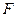 。
。
(1)求证: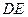 是圆
是圆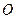 的切线;
的切线;
(2)若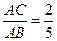 ,求
,求 的值。
的值。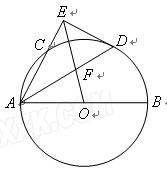
(本小题满分12分)已知函数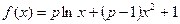 .
.
(1)讨论函数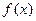 的单调性;
的单调性;
(2)当 时,
时,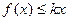 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)证明: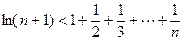
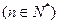 .
.
(本小题满分12分)已知点 ,过点
,过点 作抛物线
作抛物线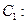
 的切线
的切线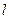 ,切点
,切点 在第二象限,如图.
在第二象限,如图.
(Ⅰ)求切点 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为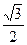 的椭圆
的椭圆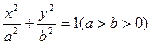 恰好经过切点
恰好经过切点 ,设切线
,设切线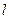 交椭圆的另一点为
交椭圆的另一点为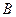 ,记切线
,记切线 的斜率分别为
的斜率分别为 ,若
,若 ,求椭圆方程.
,求椭圆方程.